10/25-x^2 - 1/5+x - x/x-5 = 0
По формулам сокращенного умножения (а^2 - в^2) = (а + в)(а - в)
10/(5-х)(5+х) - 1/(5+x) + x/(5-х) = 0 (здесь поменяли знак на +, и дробь изменилась)
Общий знаменатель (5-х)(5+х)
Получаем в числителе Знаменатель
10-5+х+5х+х^2 = 0 (5-х)(5+х) не равно 0
х^2+6х+5 = 0 5-х не равно 0, х не равен 5
Д = 36-4*1*5 = 36-20 = 16 5+х не равно 0, х не равен -5
х1 = (-6+4) / 2 = -1
х2 = (-6-4) / 2 = -5 не берем
ответ: х = -1
a)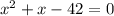
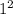-4*1*(-42)=1-4*(-42)=1-(-4*42)=1-(-168)=1+168=169;
=
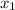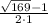=(13-1)/2=12/2=6;
= 
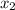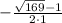=(13-1)/2=12/2=6 =(-13-1)/2=-14/2=-7.
Ищем дискриминант:
D=
Дискриминант больше 0, уравнение имеет 2 корня:
б)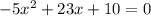
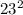-4*(-5)*10=529-4*(-5)*10=529-(-4*5)*10=529-(-20)*10=529-(-20*10)=529-(-200)=529+200=729;
= 
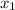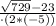=(27-23)/(2*(-5))=4/(2*(-5))=4/(-2*5)=4/(-10)=-4/10=-0.4;
Ищем дискриминант:
D=
Дискриминант больше 0, уравнение имеет 2 корня:
в)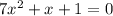
Ищем дискриминант:
D=
Дискриминант меньше 0, уравнение не имеет корней.
г)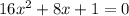
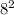-4*16*1=64-4*16=64-64=0;
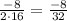=-0.25
Ищем дискриминант:
D=
Дискриминант равен 0, уравнение имеет 1 корень:
X=