ответ: 1, 2, 3
Объяснение:
7х>4
х<4
Из первого неравенства у нас х не может быть меньше 4/7, то есть всё, что больше - его решения. Это все целые числа начиная с 1
Из второго - х не превосходит 4. То есть целые решения - все целые числа не более 3. Ищем пересечения решений у обоих неравенств: это числа 1, 2, 3. Что и является ответом
1210
Объяснение:
Двухзначные числа, которые делятся на 4 с остатком 1 — это числа, которые делятся на 4 и ещё мы к ним добавляем 1 (13, 17, 21 и т.д.)
всего таких чисел 22. Самое первое число — 13, последнее — 97. И тут мы воспользуемся методом Гауса. Это метод, когда пары чисел с конца и с начала дают одно и тоже число. и тогда можно просто поделить на 2 количество чисел, посчитать количество пар и умножить их количество на сумму первого и последнего числа.
Вернёмся к задаче. Так как 97+13=110, а пар у нас 22:2=11, то достаточно умножить 110 на 11. Это будет 1210. Вот и ответ!
-14
Объяснение:
Условие задачи написано не корректно, то что вы написали можно по разному прочитать, но я всё же думаю, что вы имели в виду это:
(
) * 
.
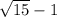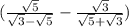С первой скобкой ничего не поделаешь, но во второй скобке можно привести всё к общему знаменателю 
.
() * = () * 
.
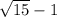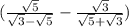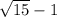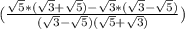Далее во второй скобке раскрываем скобки в числители и знаменателе.
() * = () * 
.
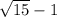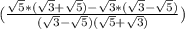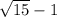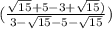Во второй скобке после элементарных арифметических операций получаем:
() * = () * 
.
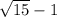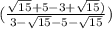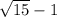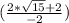Во второй скобке сократим числитель и знаменатель на 2, получаем:
() * = () * 
= () * 
=
= 
= 
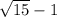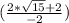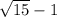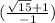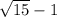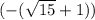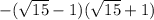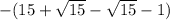= -14.
Три целых числа : 1 ; 2 ; 3