V(t) = S'(t) = -12t + 6t².
А) Подставляем t = 3 в полученное уравнение.V(3) = -12 × 3 + 6 × 3² = -36 + 6 × 9 = -36 + 54 = 18.
Б) Подставим V = 0 в уравнение зависимости скорости.-12t + 6t² = 0;
6t × (t- 2) = 0;
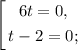
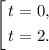
Таким образом скорость будет равна нулю в момент времени: t = 0 и t = 2.
В) Подставим V = 18 в уравнение зависимости скорости.По сути этот пункт можно не решать, ведь он уже решён в А. Но давайте всё же рассмотрим и его.
-12t + 6t² = 18;
6t² - 12t - 18 = 0;
t² - 2t - 3 = 0;
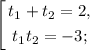
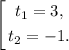
Так как время отрицательным быть не может, t₂ - посторонний корень.
Значит, искомое время 3.
ответ: 18; 0 и 2; 3.
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)