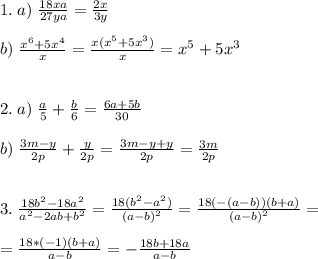

Объяснение:
Построить график функции
у=2×|х|+3
Шаг 1.
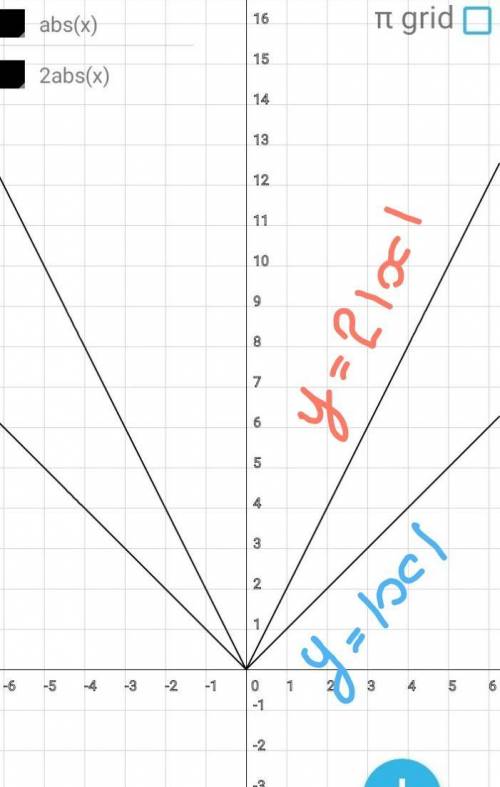
Строим график функции
у=|х|
Графиком являются биссектрисы
1 и 2 координатных четвертей.
Весь график расположен в верхней
полуплоскости.
Шаг 2.
Нужно изменить угол наклона вет
вей графика.
Построим и заполним таблицу:
у=2×|х|
х 0 -2 2
у 0 4 4
Строим график фунеции
у=2×|х|.
Шаг 3.
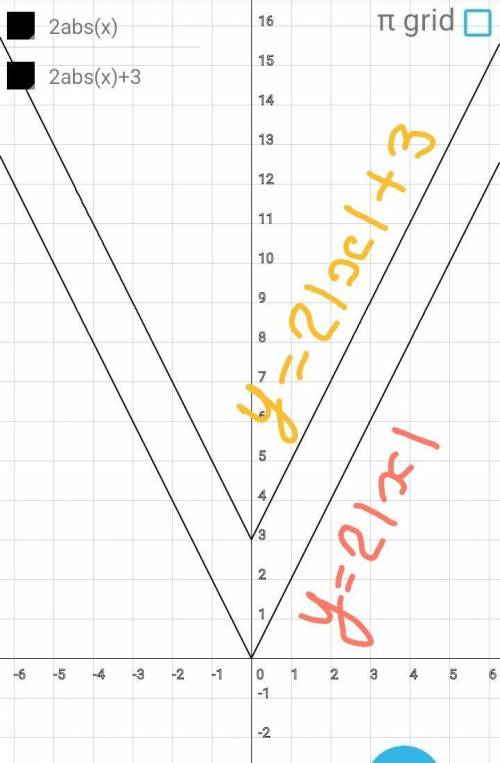
Строим график функции
у=2×|х|+3
График функции у=2×|х| поднимаем
вверх на 3 единицы ( совершаем па
раллельный перенос вдоль положи
тельного направления ОУ на 3ед. от
резка).
Построен искомый график.
Объяснение:
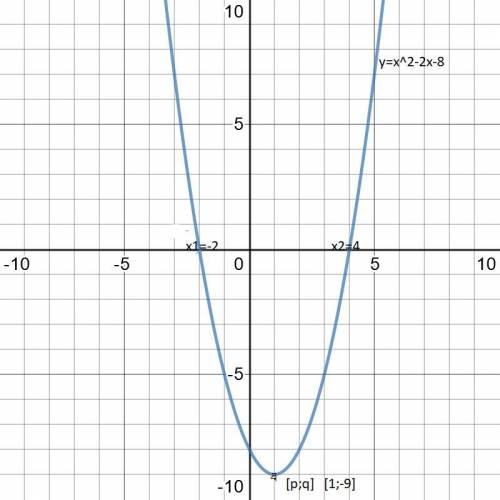
y=x²-2x-8
*ODZ : (-∞;∞)
*Набор значений: <-9;oo)
*Коэффициент a > 0 , Таким образом, функция убывает в интервале (-oo; 1> и увеличивается в интервале <1; oo)
*экстремумы: минимум для f (1)
*место пересечения функции с осью OY [0; -8]
f(0)=1*0^2-2*0-8
f(0)=-8
*вершина параболы (экстремум): [p; q]
p=-b/2a , q=-D/4a
p=- -2/2*1=2/2=1
q=-36/4*1=-36/4=-9
*нулевая позиция функции
X²-2x-8=0
Δ=(b²-4ac)=4+32=36
√Δ=6
x1=(2-6)/2=-4/2=-2
x2=(2+6)/2=8/2=4
x ∈ {-2;4}
( w załączeniu grafik funkcji kwadratowej)
Действия с дробями...