Так как члены представляют собой арифметическую прогрессию, то a2=a1+d, a5=a1+4d, где d - знаменатель арифметической прогрессии. Но так как эти же члены являются членами геометрической прогрессии, то a2=a1*q и a5=a1*q², где q - знаменатель геометрической прогрессии. По условию, a2+1=a1+1+d1, a5-3=a1+1+2d1, или a2=a1+d1, a5=a1+4+2d1. Из первого уравнения находим d1=d. Так как a5=a1+4d, то из второго уравнения следует уравнение 4d=4+2d, откуда d=2. Теперь, заменяя a2 на a1+2 и a5 на a1+8, получаем уравнения a1+2=a1*q, a1+8=a1*q². Из первого уравнения следует a1=2/(q-1). Подставляя это выражение во второе уравнение, приходим к квадратному уравнению q²-4q+3=0. Дискриминант D=(-4)²-4*1*3=4=2². Отсюда q=(4+2)/2=3 либо q=(4-2)/2=1. Но если q=1, то все члены геометрической прогрессии, а с ней и все члены исходной арифметической прогрессии, были бы равны, что было бы возможно лишь при d=0. Но так как d=2≠0, то q≠1. Значит, q=3. Тогда a1=2/(3-1)=1, и искомая сумма S100=100*(a1+a100)/2=50*(a1+a100). Но a100=a1+99d=1+99*2=199, и тогда S100=50*(1+199)=10 000. ответ: 10 000.
См объяснение
Объяснение:
а) так как перед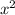
стоит положительный коэффициент (равный единице), следовательно ветви параболы направлены вверх
б) координаты вершины (x0, y0) вычисляются по формуле:
x0 =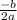
= 
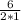= 3
y0 = y(x0) = 9 - 6*3 +5 = -4
Значит, координаты вершины : (3, -4)
c) Ось симметрии задается уравнением: x = 3
d) По теореме Виета:
Если x1, x2 - корни квадратного уравнения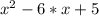
, ТО
Отсюда получаем корни x1 = 1; x2 = 5
Эти корни и есть нули функции
e) Дополнительные точки можно найти путем подстановки любых чисел: например, пусть x=0. тогда y = y(0) = 5
f) см прикрепленный рисунок