![acosx-bcos2x1,\\acosx-b(2cos^2x-1)-10,\\\boxed{t:=cosx \Leftrightarrow t \in [-1;1]}\\at-b(2t^2-1)-10,\\2bt^2-at-b+1](/tpl/images/0685/7710/b234d.png)
Переформулируем задачу:
Существуют ли числа a и b, такие, что 2bt² - at - b + 1 < 0 при любом t ∈ [-1; 1]?
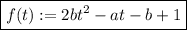
0 ∈ [-1; 1] ⇒ f(0) = 2b·0² - a·0 - b + 1 = 1 - b < 0 ⇔ b > 1.
Тогда при b > 1, график y = f(t) - парабола с ветвями вверх. Значит, решение неравенства f(t) < 0 имеет вид: (t₁; t₂), где t₁, t₂ - корни f(t).
По условию задачи должно выполняться: [-1; 1] ⊂ (t₁; t₂). То есть меньший корень должен быть меньше -1, а больший - больше 1. Для этого необходимо и достаточно, чтобы
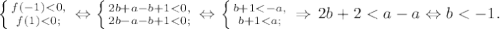
Но, как выяснилось ранее, b > 1 - противоречие.
ответ: нет.
объяснение:
№5 если в выпуклом четырёхугольнике диагонали равны и равны две противоположные стороны, то по признаку он или прямоугольник, или квадрат, или равнобокая трапеция.
в прямоугольнике и в квадрате диагонали,пересекаясь, делятся пополам, ⇒ ао=до, как половины равных отрезков.
если имеем равнобокую трапецию,то из равенства треугольников, имеющих своими сторонами основание ад и диагонали, получим равные угла между диагоналями и основанием ад ⇒δаод- равнобедренный и ао=од (замечание: чертёж, представленный в неверен, т.к. диагонали преломляются).
№6. т.к. противоположные стороны попарно равны ⇒ четырёхугольник - параллелограмм по признаку ⇒ диагонали точкой пересечения делятся пополам по свойству диагоналей параллелограмма.