Один з катетів прямокутного трикутника на 1 см меньший від другого. Знайдіть периметр трикутника, якщо його гіпотенуза дорівнює 5 см

👇

Увидеть ответ

Открыть все ответы

Ответ:

Vlad010934

27.01.2023

1) 5k+1

2) 36

3) 3186

Объяснение:

1) искомое натуральное число имеет вид: 5k+1, где k∈N₀ (k - натуральное, либо 0)

2) подставляем вместо k возможные значения:

а) k=0 ⇒ 5*0+1=1

б) k=1 ⇒ 5*1+1=6

в) k=2 ⇒ 5*2+1=11

г) k=3 ⇒ 5*3+1=16 и т.д.

замечаем, что каждое следующее число больше предыдущего на 5, то есть имеем арифметическую прогрессию, где а₁=1; d=5

чтобы определить сколько таких чисел (n) нужно, воспользуемся формулой n-го члена:

a_n=a_1+(n-1)d

по условию у нас последний член не обязательно должен равняться 180, а только не должен его превышать (an≤180), значит запишем неравенство:

$a_1+(n-1)d\leq 180 \\ \\ 1+(n-1)*5\leq 180 \\ \\ (n-1)*5\leq 179 \\ \\ n-1\leq \frac{179}{5} \\ \\ n\leq \frac{179}{5} +1 \\ \\ n\leq 36.8$

наибольшее значение n, удовлетворяющее неравенству равно 36.

Значит всего 36 таких чисел.

3) при полученном n, находим an

$a_{36}=1+(36-1)*5=176$

находим сумму по формуле:

$S_n=\frac{a_1+a_n}{2}*n \\ \\ S_{36}=\frac{1+176}{2}*36= 3186$

4,7(67 оценок)

Ответ:

bonbino1

27.01.2023

1. ОТВЕТ: например, 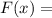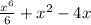F(x)= $\frac{x^6}{6}+x^2-4x$ , поскольку F'(x) = f(x) .

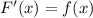Общий вид первообразных - 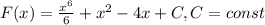$F(x)=\frac{x^6}{6}+x^2-4x+C, C=const$

2. Докажем, что 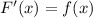F'(x)=f(x) :

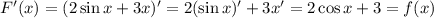$F'(x)=(2\sin x+3x)'=2(\sin x)'+3x'=2\cos x+3=f(x)$ .

Что и требовалось доказать.

3. Общий вид первообразных функции 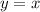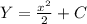y=x - $Y=\frac{x^2}{2}+C$ , где 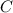- некоторое постоянное число. Если график первообразной проходит через точку 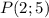P(2;5) , то это значит, что при подстановке 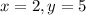x=2, y=5 получим верное равенство:

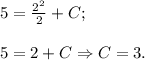
$5=\frac{2^2}{2}+C;\\\\5=2+C\Rightarrow C=3.$

Искомая первообразная - 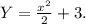$Y=\frac{x^2}{2}+3.$

ОТВЕТ: Y = x²/2 + 3.

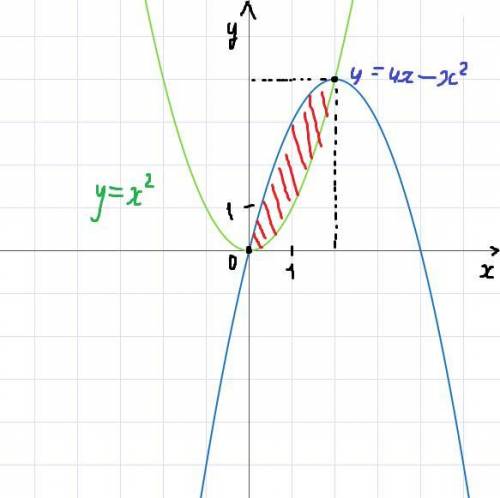
4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.

Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид

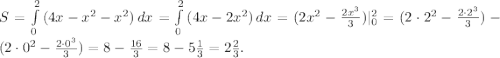
$S=\int\limits^2_0 {(4x-x^2-x^2)} \, dx =\int\limits^2_0 {(4x-2x^2)} \, dx =(2x^2-\frac{2x^3}{3})|^2_0=(2\cdot2^2-\frac{2\cdot2^3}{3})-(2\cdot0^2-\frac{2\cdot0^3}{3})=8-\frac{16}{3}=8-5\frac{1}{3}=2\frac{2}{3}.$

ОТВЕТ: 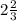$2\frac{2}{3}$ кв. ед.

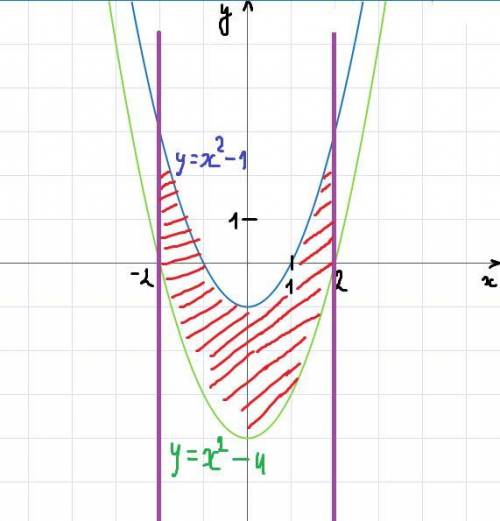
5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.

Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид

$S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12$

ОТВЕТ: 12 кв. ед.

6. Объем выполненной работы A(t) с момента 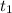t_1 по момент 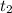t_2 согласно механическому смыслу определенного интеграла есть значение выражения интеграла

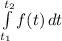
$\int\limits^{t_2}_{t_1} {f(t)} \, dt$

Имеем:

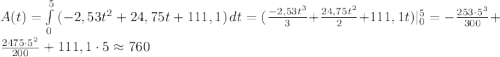
$A(t)=\int\limits^5_0 {(-2,53t^2+24,75t+111,1)} \, dt=(\frac{-2,53t^3}{3}+\frac{24,75t^2}{2}+111,1t)|_0^5=-\frac{253\cdot5^3}{300}+\frac{2475\cdot5^2}{200}+111,1\cdot5\approx760$