-x² ≤ 3 - 4x⇒x²-4x+3≥0
По Виету х=3;х=1
Решим неравенство методом интервалов.
13
+ - +
х∈(-∞;1]∪[3;+∞)
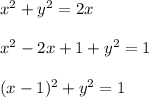
Это уравнение окружности с центром (1;0) и радиусом R = 1.
Пусть общий вид неизвестной прямой y = kx + b. Эта прямая параллельна прямой x + 2y = 0, т.е. у параллельных прямых угловые коэффициенты равны: k = -0.5. Получаем y = -0.5x + b. Известно, что прямая y = -0.5x + b проходит через центр окружности (1;0), т.е., подставляя координаты точки центра окружности, мы найдем коэффициент b
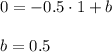
Таким образом, нашли неизвестную прямую y = -0.5x + 0.5 или x + 2y - 1 = 0
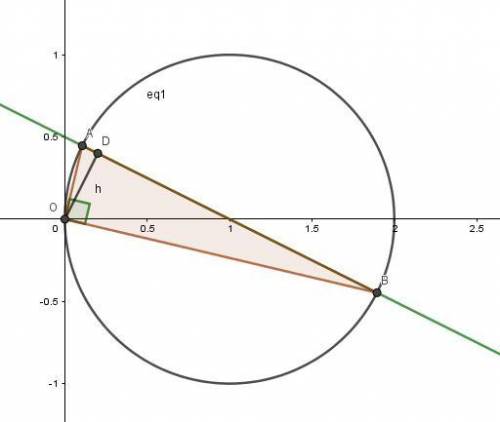
Наглядно нарисуем графики и данный треугольник.
Найдем уравнение прямой, проходящей через точку O(0;0) и перпендикулярно прямой x + 2y - 1 = 0.
Прямая, проходящая через точку M(x₀;y₀) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнением:
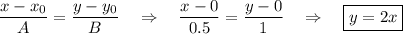
Далее найдем координаты точки пересечения двух прямых y = -0.5x + 0.5 и y = 2x.
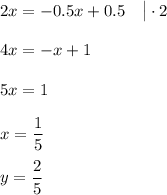
Точка D имеет координаты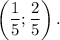 
. Расстояние от точки О до точки D:
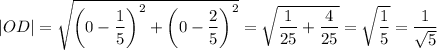
∠AOB опирается на диаметр AB, следовательно, ∠AOB = 90°, а диаметр окружности в два раза больше радиуса, т.е. AB = 2R = 2 * 1 = 2.
Площадь треугольника AOB:
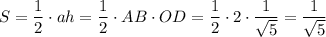кв.ед.
ответ: 1/√5 кв. ед..
Координаты точек состоят из двух чисел: первое - абсцисса (значение х), второе - ордината (значение у).
Если в выражение функции поставить вместо х абсциссу точки а вместо у - ординату этой точки и, в результате, получится верное равенство, то эта точка принадлежит графику данной функции:
А(0,5; 4) 4 = -3 · 0,5 - 6
4 = -7,5 - равенство не соблюдается, значит точка А
не принадлежит графику этой функции.
В(-3; -3) -3 = -3 · (-3) - 6
-3 = 3 - равенство не соблюдается, значит точка В
не принадлежит графику этой функции.
ответ: x ∈ (-∞;1]∪[3;+∞)
-x^2 ≤ 3 - 4x
4x - x^2 - 3 ≤ 0
-x^2 + 4x - 3 ≤ 0 |-1
x^2 - 4x + 3 ≥ 0
x^2 - 4x + 3 = 0
D = b^2 - 4ac = 16 - 12 = 4
x1,2 = (-b +/-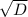
)/2a
x1 = (4 + 2)/2 = 3
x2 = (4 - 2)/2 = 1
Построение на картинке