Алгебра: Розвʼязати систему рівнянь зручним х-у=3 3х-2у=-8

Розвʼязати систему рівнянь зручним х-у=3 3х-2у=-8

👇

Увидеть ответ

Открыть все ответы

Ответ:

Ok7a

11.10.2020

В обоих случаях нужно делать замену переменной.

$\displaystyle \int\limits^{\frac{\pi}{6}}_0 {e^{sin(x)}}\cdot cosx \, dx$

Что тут можно предпринять? Известно,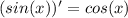 (sin(x))' = cos(x) , вот и сделаем замену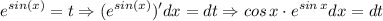 $\displaystyle e^{sin(x)} = t \Rightarrow (e^{sin(x)})'dx=dt \Rightarrow cos\, x\cdot e^{sin \, x} dx=dt$

Вообще идеально, получим простейший интеграл. Так как это определенный интеграл, то обратную замену можно не делать, а просто пересчитать пределы по самой замененной функции

$\displaystyle e^{sin\, 0} = e^0=1 \\ e^{sin \, \frac{\pi}{6}} = e^{0.5}=\sqrt{e}$

То есть пределы станут: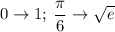 $\displaystyle 0 \to 1; \: \frac{\pi}{6} \to \sqrt{e}$

А теперь сам интеграл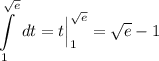 $\displaystyle \int\limits^{\sqrt{e}}_1 {} \, dt = t \Big|\limits^{\sqrt{e}}_1 = \sqrt{e} -1$

Теперь следующий интеграл:

$\displaystyle \int\limits^5_1 {\frac{x}{\sqrt{1+3x}} } \, dx$

Что можно такого заменить? Попробуем взять корень, его производная даст тот же корень в знаменателе, да и сам вполне нормально выражается, делаем:

$\displaystyle \sqrt{1+3x}=t \Rightarrow \frac{3}{2\sqrt{3x+1}}dx=dt \\ 1+3x=t^2 \Rightarrow x=\frac{t^2-1}{3}$

Заодно сразу новые пределы посчитаем:

$\sqrt{3\cdot 1+1} = \sqrt{4}=2 \\ \sqrt{3\cdot 5+1} = \sqrt{16}=4$

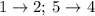
То есть $1 \to 2; \: 5 \to 4$

Теперь подставляем и смотрим, что получается:

$\displaystyle \int\limits^4_2 {\bigg(\frac{t^2-1}{3} \bigg)\cdot \frac{2}{3} } \, dt=\frac{2}{9}\int\limits^4_2 {(t^2-1)} \, dt =\frac{2}{9}\bigg(\frac{t^3}{3}-t \bigg) \bigg|\limits_2^{4}=\\=\frac{2}{9}\cdot \bigg(\frac{4^3}{3}-4\bigg)-\frac{2}{9}\bigg(\frac{2^3}{3}-2 \bigg)=\frac{2}{9}\bigg(\frac{64}{3}-\frac{12}{3}-\frac{8}{3}+\frac{6}{3} \bigg)=\frac{2}{9}\cdot \frac{50}{3}=\frac{100}{27}$

Можно, конечно, было и получить неопределенный интеграл и в него подставить старые пределы, но пересчет на новые позволяет не совершать часть действий

4,5(1 оценок)

Ответ:

Дубак113

11.10.2020

24÷4=6 (км/ч) скорость лодки по течению реки.

24÷6=4 (км/ч) скорость лодки против течения реки.

6-4=2 (км/ч) удвоенная скорость течения реки.

2÷2=1 (км/ч) скорость течения реки.

6-1=5 (км/ч) собственная скорость лодки.

ответ: 5 км/ч собственная скорость лодки; 1 км/ч скорость течения реки.

Решение уравнением:

Пусть х (км/ч) скорость течения реки, тогда собственная скорость катера по течению реки будет 24÷4-х=6-х (км/ч), а против течения 24÷6+х=4+х . Т.к. собственная скорость катера неизменна, составим уравнение:

6-х=4+х

2х=2

х=1 (км/ч) скорость течения реки.

6-1=5 (км/ч) собственная скорость катера.

ответ: 5 км/ч собственная скорость лодки; 1 км/ч скорость течения реки.

4,4(38 оценок)

Это интересно:

Компьютеры-и-электроника

11.11.2020

Легкий способ - как скопировать музыку с CD в формате MP3...

Компьютеры-и-электроника

17.06.2022