7 класс Алгебра СОР 06.05
Вариант 2
1. Преобразуйте в многочлен.
а) (3a + 4)2; в) (b + 3) (b – 3);
б) (2x – b)2; г) (5y – 2x) (5y + 2x).
2. У выражение
а)(c + b) (c – b) – (5c2 – b2);
б) (x + y) (x – y) – (x2 + 3y2).
3. Разложите на множители.
а) 25y2 – a2; б) c2 + 4bc + 4b2.
4. Решить уравнение:
а) х+3х=0;
б) (3х+4)-(3х+1)(3х-1)=49.
5. Вычислите: 8,8-1,2
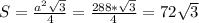условных единиц площади
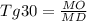⇒ MO=MD*Tg30°=
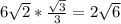условных единиц длины
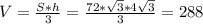условных единиц объема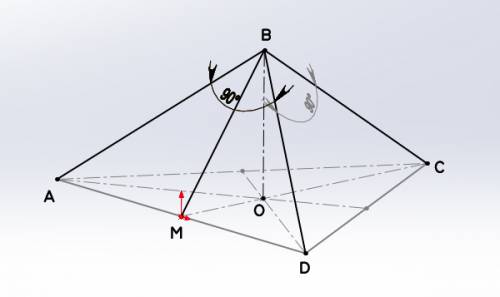
∠ABD=∠DBC=∠CBA=90°
Рассмотрим ΔABD. Он равнобедренный т.к. AB=BD.
Найдем сторону основания AD по теореме Пифагора
AD²=AB²+BD² ⇒ AD=√(12²+12²=√2*144=12√2 условных единиц длины.
ΔADC - равносторонний, так как ΔABD=ΔDBC=ΔABC
Площадь равностороннего треугольника
Проведем из точки B на сторону AD высоту в точку M (она же медиана и биссектриса).
∠ABM=∠BAM=∠ADB=∠DBM=45°
MB=AM=0,5AD=6√2 условных единиц длины
В основании в равностороннем треугольники проведем из его вершин высоты (они же медианы, биссектрисы).
Рассмотрим Δ MOD (∠MDO=30° , так как все углы в равностороннем треугольнике равны 60°, а биссектриса проведенная из вершины делит угол пополам):
BO²=MB²-MO² ⇒ BO=√(72-24)=4√3 условных единиц длины
Объем пирамиды равен