Нам нужно доказать, что √17 является иррациональным числом. Пусть оно является рациональным числом. Тогда его можно представить в виде m/n, где m ∈ Z, n ∈ N и дробь несократимая. Возведя в квадрат, получаем, что 17 = m²/n² Тогда 17n² = m² Чтобы равенство было верным, необходимо, чтобы m ⋮ 17 тогда и n ⋮ 17, иначе данное равенство будет неверным, т.к. 17 - простое число. Тогда дробь m/n будет сократимой, т.к. и числитель, и знаменатель кратны 17. Но это невозможно, поэтому дробь вида (m/n)² = 17 не существует ⇒ число 17 не может являться квадратом рационального числа, т.е. √17 - иррациональное число.
Выразим в первом уравнении переменную "у". Для этого нужно перенести неизвестную в правую часть и сменить ее знак. Получим:
Подставим данное значение "у" в уравнение "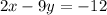
". Получим:
Рапределяем "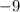
" через скобки. Получим:
Приводим подобные члены. Получим:
Переносим постоянную в правую часть и сменяем ее знак. Получим:
Вычисляем разность. Получим:
Делим обе стороны уравнения на "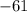
". Получим:
Подставляем данное значение "х" в уравнение "у=-19+7х". Получим:
Умножаем числа. Получим:
Вычисляем сумму. Получим:
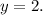
ОТВЕТ: решением данной системы уравнений является пара чисел "