Судя по содержанию учебника, комбинаторику и теорию вероятности в решении применять нежелательно?..)) Тогда так:
Для выполнения условия необходимо, чтобы:
1-й ученик получил тетради 2; 3 или 4
2-й ученик получил тетради 1; 3 или 4
3-й ученик получил тетради 1; 2 или 4
4-й ученик получил тетради 1; 2 или 3
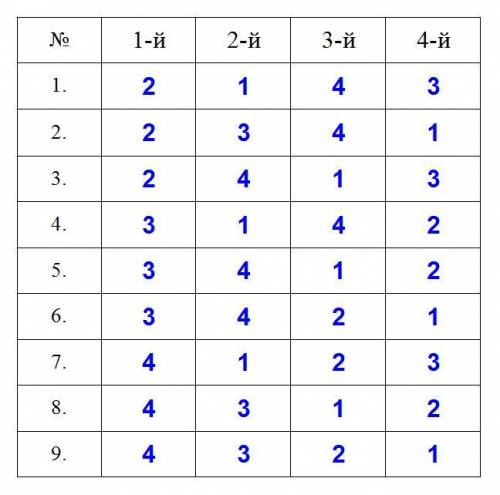
Все возможные варианты раздачи тетрадей ученикам так, чтобы ни один из них не получил свою тетрадь (числа обозначают номера тетрадей, в верхней строке - номера учеников): см. рис.
Как видно из таблицы, всего таких вариантов - 9.
Поскольку речь в задании идет не о величине вероятности, а о вариантах вероятности, то, скорее всего, ответ нужен именно такой.
Напишем числа в столбик
Посмотрим на сумму третьих цифр, она должна равняться 2 или 12, или 22.
7+3 =10, значит, ни 2, ни 22 как сумма не подходят (2<10, и ни одно однозначное число до 22 не доберёт. Значит, сумма должна быть равна 12, а число 12-10=2).
Таким образом, второе число 22204. Так как 12>10, единицу держим в уме, она переходит в сумму вторых чисел.
Посмотрим на сумму вторых цифр.
Она должна равняться 7,17 или 27.
5+2 уже семь, а у нас ещё единица в уме, итого уже восемь. До семнадцати можно достать однозначным числом 17-8=9, значит, вторая цифра девятка.
Единицу от 17 опять держим в уме.
Сумма первых чисел или 5,или 15,или 25.
1+2=3 + единица в уме = 4. Достаём однозначным числом только до пятерки, поэтому 5-4=1 и третье число 19331.
Проверяем
15728+22204+19331=57263