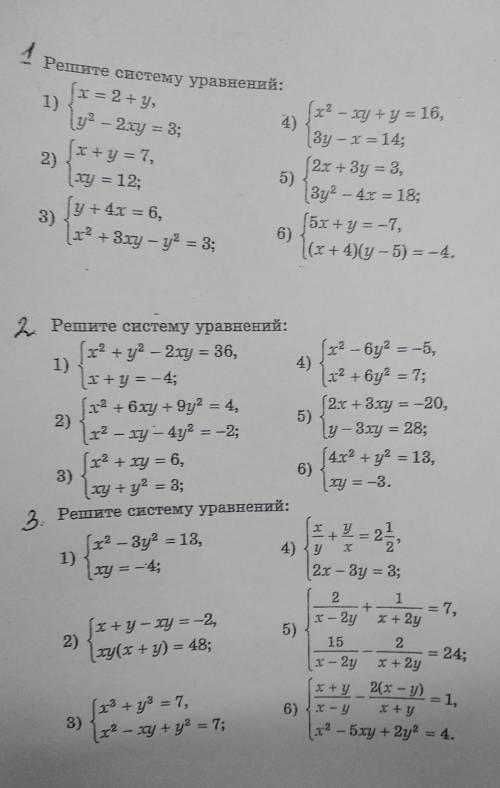
Дано:
ромб ABCD
угол BAD = 120°
AC — диагональ
AC = 8см
Найти: периметр (P) ромба
P = 4a, где a — сторона ромба.
Проведем диагональ BD.
Так как, по свойству ромба, диагонали ромба являются биссектрисами, то угол BAO = углу OAD = 1/2 угла BAD = 120°/2 = 60°.
По свойству ромба, диагонали ромба перпендикулярны и в точке пересечения делятся пополам, значит угол AOD = 90°, а AO = OC = 1/2 AC = 8см / 2 = 4см.
Треугольник AOD — прямоугольный. Сумма углов треугольника равна 180°, значит угол AOD + угол ODA + угол OAD = 180°
угол ODA = 180° – угол AOD – угол OAD = 180° – 90° – 60° = 30°.
По свойству прямоугольного треугольника, катет, лежащий против угла 30°, равен половине гипотенузы. Значит, AO = 1/2 AD, AD = 2*AO = 2*4см = 8см.
Так как все стороны ромба равны, по свойству ромба, то P = 4 * 8см = 32см
ответ: 32 см
всё сделать не получится, но я попробую объяснить
Пошаговое объяснение:
умножаешь левую часть первого уравнения в системе на левую часть второго уравнения в системе. Так же делаешь с правой часть уравнения. пример:
{у+3= 7
{y+6=10
(y+3)*(y+6)=7*10