1.
то что показано как решать неэффективно
x² + y² + 2y - 9 = 0
3x - y - 1 = 0
y² + 2y + 1 + x² - 10 = 0 (1)
y = 3x - 1 (2)
(y + 1)² + x² = 10 и подставляем из (2)
(3x - 1 + 1)² + x² = 10
9x² + x² = 10
x² = 1
x = ± 1
x = 1 y = 3x - 1 = 2
x = -1 y=3x - 1 = -4
ответ (1, 2) (-1, -4)
2)
x² - 4x - 5 < 0
3x - 9 > 0
разложим на множители x² - 4x - 5 = (x - 5)(x + 1)
D = 16 + 20 = 36
x12 = (4 +- 6)/2 = 5 -1
(x + 1)(x - 5) < 0
3(x - 3) > 0
Применяем метод интервалов
(-1) (5)
(3)
x ∈ (-1, 5) ∩ (3, +∞)
ответ x ∈ (3, 5)
3)
подкоренные выражения ≥ 0
x - 3 ≥ 0
x² -7x + 6 ≥ 0
раскладываем второе
D = 49 - 24 = 25
x12 = (7 +- 5)/2 = 6 1
x² -7x + 6 = (x - 1)(x - 6)
Применяем метод интервалов
[1] [6]
[3]
x ∈ {(-∞, 1] U [6, +∞)) ∩ (3, +∞)
ответ x ∈ [6, +∞)
1) 4
2) 3
3) 4
4) -10,4 -11,4 -10,9 -10,7 (решения такие, но хз что выбрать)
5) 1
6) 1/5 -8 = 0,2-8 = -7,8
7) раскрываем скобки 5х-18-9х<-8x-6
приводим подобные члены -4-18<-8x-6
переносим неизвестную в левую часть и меняем знак-4x-18+8x<-6
переносим постоянную в правую часть и меняем знак -4x+8x<-6+18
приводим подобные члены 4x<-6+18
вычисляем сумму 4x<12
разделяем обе части неравенства на 4 x<3
x э (-8,3)
8) 7+2v21+3-2v21
7+3
10
9) сори, не знаю
10) на скринах
Объяснение:
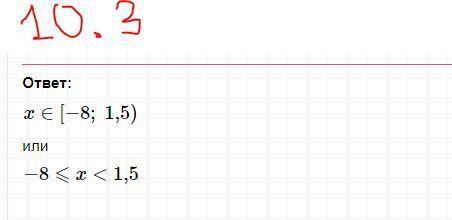
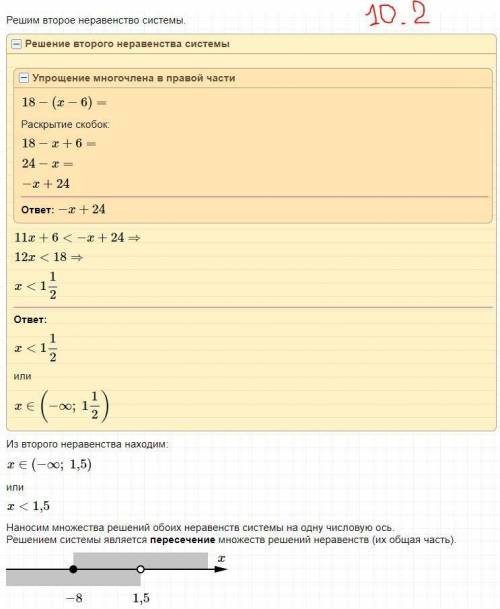
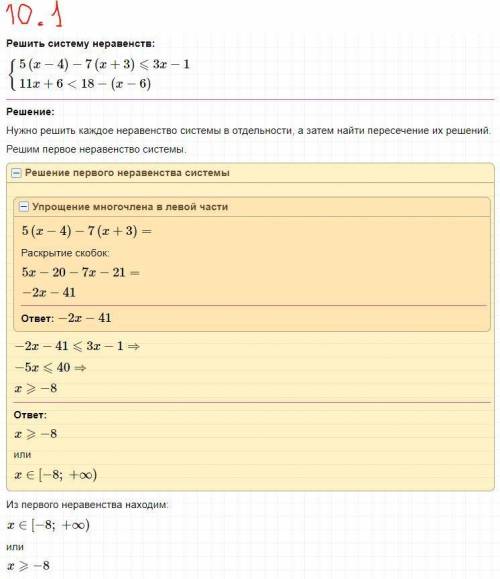
За еденичный отрезок берём 1 клетку тетрадного листа