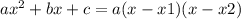
Найдём корни данного уравнения
Тут нет корней, так как дискриминант отрицательный.
придётся немного поработать с «подбором»:
пусть сначала было k коробок, потом n, затем m.
тогда: 6k = 9n + 6,
а также
6k = 7m + 3.
или:
9n + 6 = 7m + 3.
выразим отсюда: n = (7m – 3)/9.
но n (равно как и k и m) должно быть целым. подбираем варианты:
m = 3 => n = 2; (m увеличиваем в каждом шаге на 9)
m = 12 => n = 9; k = 1,5n + 1 = 14,5.
m = 21 => n = 16; k = 24 + 1 = 25.
m = 30 => n = 23; k = 34,5.
m = 39 => n = 30; k = 45 + 1 = 46.
при k = 25 имеем: 6k = 150, это < 200.
при k = 46 получаем: 6k = 276.
то число подарков «подходит» под условие .
проверяем: 306 = 9•30 + 6 =276; 306 = 7•39 +3 = 276.
итак, число подарков было

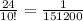

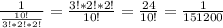
Объяснение:
Эм, тут нет корней, D отрицательный