{7x+y=20(умножим на 5)
{x-5y=8
{35х+5у=100
{х-5у=8
Прибавляем столбиком при этом - 5у с 5у сокращаются.
36х=108
Х=3
Подставляем вместо х:
7*3+у=20
21+у=20
У=20-21
У=-1
ответ:х=3;у=-1
Объяснение:
1)
a) нет (любое отрицательное целое число не является натуральным, например -1)
б) да
в)нет ( например число 1,25)
г)Нет (например число √7 будет действительным и иррациональным)
3) 
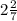= 16/7 = 160/70
2,2 = 22/10 = 144/70, значит 16/7>2,2
2,3 = 23/10 = 161/70, значит 16/7<2,3 , а значит правильный ответ 2 ( не знаю почему учитель поставил -, наверное ошибся)
ответ: 2
4) Площадь прямоугольника находится по формул S = a*b, где a и b его стороны
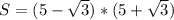тут мы видим разность квадратов
S = 5²-√3² = 25 -3 = 22
ответ : 22
5) 
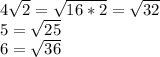
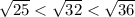, значит 4√2 находится между ними
середина между 25 и 36 - число 31, а т.к 32>31, то точка будет ближе к числу 6, а значит ответ 3)P
ответ: 3
6)
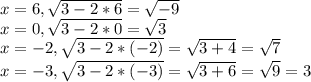
В 1 случае нет решения, т.к корень отрицательный
Во 2 и 3 корни иррациональные
В 4 уравнение мы получили число 3 - рациональное, значит ответ 4
ответ: 4
7)
a)
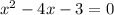
D= (-4)²-4*1*(-3) = 16 + 12 =28
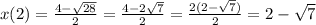- подходит
б)5x²-x = 0
x(5x-1)=0
x = 0 или 5x -1 = 0
5x = 1
x = 0,2 - не подходит, т.к тут корни уравнения рациональные
в) 1 - 4x²= 0
4x² = 1
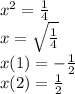- не подходит, т.к тут рациональные корни уравнения
ответ: 1
8) тут просто подставляем x и y
M: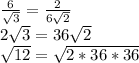 
- неверно
N: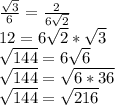 
- неверно
P: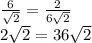 
- неверно
ну методом исключения правильный ответ 4) Q , но лучше перепроверить
Q: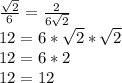
- истина
ответ: 4
1. Будем доказывать методом математической индукции.
Проверяем истинность утверждения при n = 1:
а) 2*49 + 16 + 40 = 154 = 11*14 - делится на 11.
б) Предположим, что 2*7^(2k) + 16^k +8*5^k - делится на 11. Где k - произвольное натуральное число.
в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:
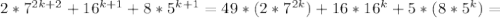
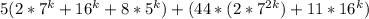
Теперь четко видно что оба больших слагаемых делятся на 11:
первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.
Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.
Значит исходное выражение делится на 11. что и требовалось доказать.
2)
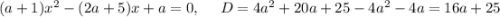
D>0 a>-25/16 a>-1,5625
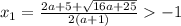
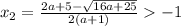
Разбиваем ОДЗ на две части:
а) (-1; беск)
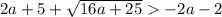
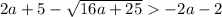
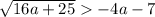
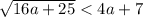
Первое из написанных неравенств верно. Проверим второе:
16a+25<16a^2+56a+49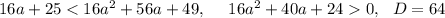
Корни -1; -1,5 Решение с учетом ОДЗ: (-1; беск)
б) (-1,5625; -1)
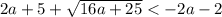
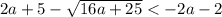
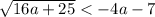
Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.
ответ: (-1; бескон).
3.
![[\sqrt{1-sin^2153}+\sqrt{tg^2207-sin^2207}]sin63=[-cos153+\frac{sin^2207}{-cos207}]sin63](/tpl/images/0025/6265/72073.png)
![=[sin63+\frac{cos^263}{sin63}]sin63=sin^263+cos^263=1](/tpl/images/0025/6265/378ae.png)
ответ: 1
ответ: 7x+y=20⇒35*х+5*у=100, тогда при сложении со вторым уравнением имеем 36*х=108⇒х=3, тогда у=20-7*3=20-21=-1.
ответ: х=3, у=-1.
Объяснение: