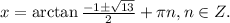Если cos²x=0, то выражение написанное сверху будет представлять из себя следующее -sin²x=0, то есть sinx и cosx=0, а значит и их сумма равна 0, но по основному тригонометрическому тождеству мы знаем, что сумма квадратов косинуса и синуса всегда равняется 0 из чего можно сделать вывод, что cos²x≠0, тогда мы можем делить на него не потеряв корни.
cosx≠0 и tanx=... всегда будут пересекаться, потому что cosx≠0 это условие существования тангенса, когда cosx=0, тангенс не определён.
Рисунок к заданию - во вложении 1. Проведем прямую через точки В и С. 2. Точку А соединим с точкой С.. 3.Вокруг отрезка [AC] нарисуем прямоугольник 1 × 2, в котором [AC] является диагональю и делит данный прямоугольник на 2 равных прямоугольныз треугольника. 4. Имеем прямоугольный треугольник с катетами длины 1 и 2 и гипотенузой [AC]. 5. По формуле Пифагора вычисляем длину гипотенузы: 1²+2²=[AC]² => [AC]²=5 => [AC]=√5 ответ:Расстояние от точки А до прямой ВС равно √5≈2.2 клетки
1) В принадлежит, если подставишь в y=-3xвместо х абсциссу точки В, а вместо у ординату точки В.
2) ответ номер 3, у=9, так как он параллелен оси х 3)5х+3·0 -15=0 5х-15=0 5х=15 х=3 точка А(3;0) -точка пересечения графика с осью ох. 4)6x-7y+12=0 вместо у подставляем нуль и считаем, 6х-7·0 +12=0 6х=-12 х=-2 это и есть абсцисса В(-2;0) -точка пересечения графика с осью ох.
Если cos²x=0, то выражение написанное сверху будет представлять из себя следующее -sin²x=0, то есть sinx и cosx=0, а значит и их сумма равна 0, но по основному тригонометрическому тождеству мы знаем, что сумма квадратов косинуса и синуса всегда равняется 0 из чего можно сделать вывод, что cos²x≠0, тогда мы можем делить на него не потеряв корни.
cosx≠0 и tanx=... всегда будут пересекаться, потому что cosx≠0 это условие существования тангенса, когда cosx=0, тангенс не определён.
ответ: