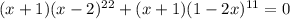
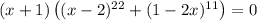
Уравнение распадается на два. Рассмотрим первое уравнение:
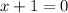
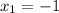
Рассмотрим второе уравнение:
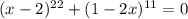
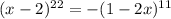
Заметим, что в левой и правой части стоят 11 степени некоторых выражений. Так как функция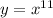 
монотонно возрастает на всей области определения, то для этой функции можно сделать вывод: значения функций равны когда равны значения аргументов. Запишем:
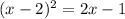
Дорешаем это уравнение:
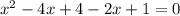
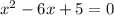
В соответствии с теоремой Виета:
Нетрудно заметить, что этим условиям удовлетворяют числа 1 и 5, но нас больше интересует именно их произведение:
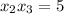
Тогда, произведение всех корней:
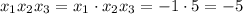
ответ: -5
Дано:
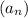- арифметическая прогрессия.
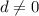
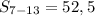
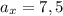
Найти: 
Решение.
1) 
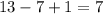- количество членов с седьмого по тринадцатый.
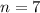
2) 
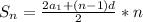формула суммы 
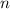членов арифметической прогрессии
Для суммы членов с седьмого по тринадцатый первым
членом будет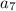 
.
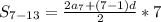
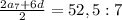
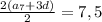
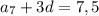
3) По формуле общего члена арифметической прогрессии
выразим 
.
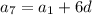Подставим в уравнение 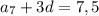и получим:
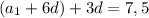
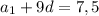
4) По условию один из членов данной прогрессии с номером
равен 7,5.
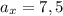иначе
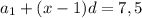
5) Очевидно, что два уравнения
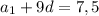и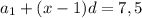
имеют равные правые части 7,5 = 7,5 , а это значит, что
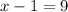
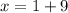
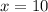
10-й член данной прогрессии равен 7,5.
ответ: 10.
Объяснение:
1-9+g=0
-8+g=0
g=8
X2-9x+8=0
X1=8
X2=1