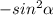Объяснение:
максимума называется локальным максимумом, значение функции в точке минимума - локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка x0 называется точкой строгого локального максимума функции y=f(x), если для всех x из окрестности этой точки будет справедливо строгое неравенство f(x)<f(x0).
Точка x0 называется точкой строгого локального минимума функции y=f(x), если для всех x из окрестности этой точки будет справедливо строгое неравенство f(x)>f(x0).
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
1)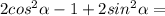
ответ:
2)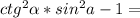
ответ: