Итак, найдем производную от нашей функции :
,
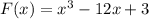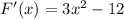
Тогда посчитаем значение производной в точке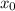 
:
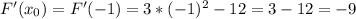
Чтобы найти наибольшее и наименьшее значение функции на отрезке необходимо найти точки экстремума функции (в этих точках функция меняет монотонность) , приравняв производную функции к 0, а затем найти значения функции на концах отрезка и в экстремумах :
1. Находим точки экстремума :
,
,
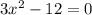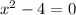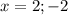
2. Находим значения функции в точках экстремума и на концах отрезка :
⇒ 
,
⇒ 
⇒ 
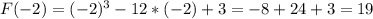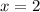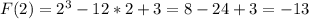
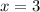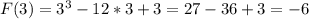
Отсюда делаем вывод, что наибольшее значение функции равно 19, оно достигается в точке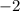 
, наименьшее значение равно -13, и оно достигается в точке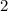 
1)(t^3 + 2t^2 + 5t +8)/t =t^2 + 2t + 5 + 8/t. Чтобы найти максимум данной функции, обратимся к ее производной и найдем точки, в которых она равна 0 либо не существует вообще.
Назовем эту функцию f(t).
f’(t)=2t+2 - 8/t^2.
f’(t)=0.
-8/t^2 +2t+2=0
-4/t^2 +t+1=0(домножим на t^2, t=0 не является корнем)
t^3+t^2-4=0.
А вот здесь я уже сам запутался, как решить это уравнение, но интернет говорит о том, что ответ здесь примерно 1,31.
Также нужно еще подумать, что будет с производной при значении t=0. По крайней мере, я навел на правильный мысли, хоть и не решил до конца)