1440 дробей.
Объяснение:
Попробуем решить системой неравенств.
Нам нужно найти все дроби с числителем 2015, чтобы выполнялось:
1/2016 < 2015/x < 1/2015
Раскладываем на два неравенства:
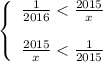
Переносим всё налево:
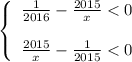
Приводим обе системы к одному знаменателю 2015*2016*x:
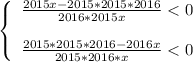
Так как x > 0, то знаменатели > 0, значит, числители < 0:
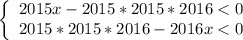
1 неравенство делим на 2015, а 2 неравенство делим на 2016:
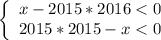
Разделяем переменные и числа:
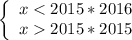
Подходят все от 2015*2015 + 1 = 4060226 до 2015*2016 - 1 = 4062239
Всего таких дробей: 4062239 - 4060226 + 1 = 2014
Но нам нужны несократимые дроби.
То есть знаменатель x не должен иметь одинаковых делителей с 2015.
2015 = 5*13*31
Его делители: 5, 13, 31, 65, 155, 403.
Рассмотрим каждый из делителей:
5: Наименьшее кратное : 4060230. Наибольшее кратное : 4062235.
Всего таких чисел : (4062235 - 4060230) : 5 + 1 = 402
13: Наименьшее кратное : 4060238. Наибольшее кратное : 4062227.
Всего таких чисел : (4062227 - 4060238) : 13 + 1 = 154
31: Наименьшее кратное : 4060256. Наибольшее кратное : 4062209.
Всего таких чисел : (4062209 - 4060256) : 31 + 1 = 64
65: Наименьшее кратное : 4060290. Наибольшее кратное : 4062175.
Всего таких чисел : (4062175 - 4060290) : 65 + 1 = 30
155: Наименьшее кратное : 4060380. Наибольшее кратное : 4062085.
Всего таких чисел : (4062085 - 4060380) : 155 + 1 = 12
403: Наименьшее кратное : 4060628. Наибольшее кратное : 4061837.
Всего таких чисел : (4061837 - 4060628) : 403 + 1 = 4
Это значит вот что.
Из 402 чисел, кратных 5, есть 30 чисел, кратных 65, то есть кратных 13.
Поэтому они вошли в два списка: кратных 5 и кратных 13.
Их надо один раз вычесть.
Также, из этих 402 чисел нужно вычесть 12 чисел, кратных 155 = 5*31.
И из 154 чисел, кратных 13, нужно вычесть 4 числа, кратных 403 = 13*31.
Таким образом, получается всего нужно вычеркнуть:
402 + 154 + 64 - 30 - 12 - 4 = 574
И всего получается:
2014 - 574 = 1440 несократимых дробей.
Объяснение:
Во всех примерах легко увидет значение х при котором и числитеь и знаменатель обращаются в 0. На такой двучлен и надо делить.
1) делим на (х-3)
получим 4/(х-2)
2) Делим на (х+3)
Получим (х+4)/х
3) делим на (х-3)
Получим (2х-1)/(х+3)
4) делим на (х-2)
Получим (х-2)/(х+7)
5) здесь немного сложнее : находим дискриминант числителя . Он равен 121
Корни 0,5 и -5. Числитель (2х-1)*(х+5)
Знаменатель (х+5)*(3х-1)
Отношение (2х-1)/(3х-1)
6) Знаменатель -2*(х*х-11х+28) по теореме Виета корни 4 и 7
Так что знаменатель -2*(х-4)(х-7).
Смотрим какой из корней обращает в 0 числитель .
это х=7 . Видим, что числитель (х-7)(5х-2)
ответ: (5х-2)/(8-2х)