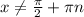
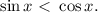
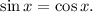 Решать его можно, деля на косинус и получая при этом уравнение относительно тангенса. Но проще вспомнить, что косинус и синус - это абсцисса и ордината точки на единичной окружности. Они равны на биссектрисе 1-го и 3-го координатных углов. Меньше же ордината будет ниже этой прямой,чему соответствуют промежутки от
Решать его можно, деля на косинус и получая при этом уравнение относительно тангенса. Но проще вспомнить, что косинус и синус - это абсцисса и ордината точки на единичной окружности. Они равны на биссектрисе 1-го и 3-го координатных углов. Меньше же ордината будет ниже этой прямой,чему соответствуют промежутки от 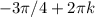 до
до 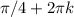 .
.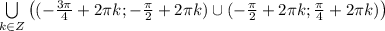
Пусть одна сторона этих прямоугольников x, а другая y.
У одного прямоугольника периметр P = 2(x + y) = 20
x + y = 10; x = 10 - y.
Приставим прямоугольники друг к другу в цепочку сторонами x.
Получим длинный прямоугольник с сторонами x и 7y
P = 2(x + 7y) = 2(10 - y + 7y) = 2(10 + 6y) = 100
10 + 6y = 50
6y = 40; y = 40/6 = 20/3 = 6 2/3; x = 10 - y = 3 1/3 = 10/3
Прямоугольник со сторонами 10/3 и 20/3 имеет периметр 20,
а 7 таких прямоугольников, выстроенных в цепочку, дают прямоугольник с периметром 100.
2) Сумма 100 = 3*33 + 1 содержит 34 хороших слагаемых.
Это и есть максимум.
3) Бред - треугольник не может быть ромбом.