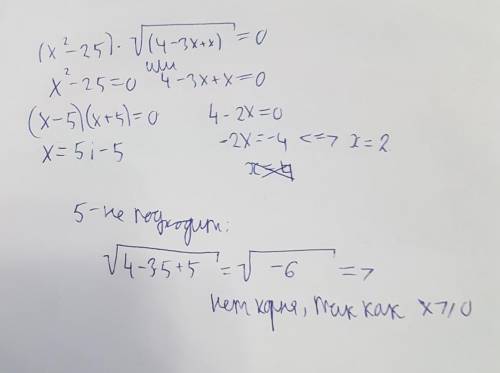
Сначала просто раскрываешь скобки:
6m+8 — из-за того, что перед скобкой ничего нет (или же можно считать, что там плюс стоит) знаки внутри не меняются
-3m+4 — из-за того, что перед скобкой минус все знаки внутри, скобки меняются
6m+8-3m+4
Находим подобные члены (с одинаковыми параметрами), у нас это 6m и -3m, а затем складываем числа 8 и 4
6m-3m+8+4=3m+12
3m делится на три, где остается 1m (1 не пишется), и 12 тоже делится на три и Остается 4. Значит можно вывести 3 за скобки
3(m+12)
Теперь это выражение можно разделить на 3. Кратное - это делимое, первое значение в делении
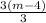
3 сверху и 3 снизу сокращаются и остается m-4. Значит это выражение является кратным трем
Предположим , что степень полинома P(x) не равна степени полинома: x*Q(x).
Тогда степень полинома:
P(x) + x*Q(x) равна либо степени полинома P(x) либо x*Q(x) , в зависимости от того степень какого полинома больше. Но тогда по условию полином большей степени должен иметь 2 степень. Соответственно полином меньшей степени имеет 1 или 0 степень. Но тогда полином : x*P(x)*Q(x) имеет 2 или 3 степень, что невозможно , тк по условию : P(x)*x*Q(x) должен иметь 9+1=10 степень. То мы пришли к противоречию .
Значит степени полиномов P(x) и x*Q(x) должны быть равны.
Тогда тк степень x*P(x)*Q(x) равна 10. То степень полинома P(x) равна:10/2=5
2) Полином :
P(x) +Q(x) имеет степень 3, а полином
P(x)-Q(x) имеет степень 5.
Тогда сумма и разность этих полиномов имеет 5 степень:
То есть 2*P(x) имеет 5 степень и 2*Q(x) имеет 5 степень.
Тогда P(x)*Q(x) имеет 10 степень.