Разложим 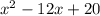 на множители с группировки.
на множители с группировки.
Разложи выражение на множители путем группировки. Сначала выражение необходимо переписать в следующем виде: x^2 +ax+bx+20. Чтобы найти a и b, настрой систему для решения.
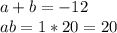
Поскольку ab положительное, a и b имеют одинаковый знак. Так как a+b отрицательный, a и b являются отрицательными. Перечисли все такие пары, содержащие 20 продукта.
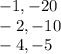
Вычисли сумму для каждой пары.
−1−20=−21
−2−10=−12
−4−5=−9
Решение — это пара значений, сумма которых равна −12.
Перепишите 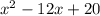 как
как 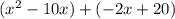
Вынесите за скобки общий член x−10, используя свойство дистрибутивности.
Получим 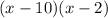
- 1/2
Объяснение:
4x^2+x-2=0
4x^2+x=2 | :4
x^2+(1/4x)=1/2
x^2+1/4x+(1/8)^2 = 1/2 + (1/8)^2
-->> тут можно показать ход вычислений, но я записываю кратко
(x+1/8)^2 = 33/64
x+1/8 = +-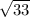 /8 (записать нужно как дробь)
/8 (записать нужно как дробь)
x1 = -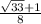
х2 =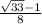
х1 * х2 = -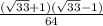 = -
= -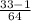 = (дробь сокращается на 32) = - 1/2
= (дробь сокращается на 32) = - 1/2