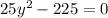
Разделить обе части уравнения на 25
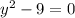
Перенести константу в правую часть равенства
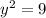
Извлечь корень
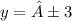
Отделить
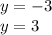
Окончательное решение
y¹= -3
y²= 3
………….
an = an-1 + d
3)
4)Пусть имеется последовательность чисел:
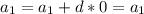проверено.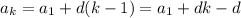
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
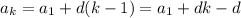то прибавив к данному выражению d. Мы получим следующий член .![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
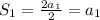. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
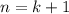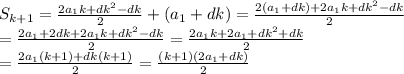
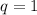получается деление на ноль, поэтому сразу пишем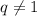 
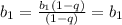
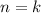
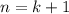:![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
25y² - 225 = 0
25y² = 225
y² = 225/25 = 9
=> y = ±3
ответ: y = ±3
Это правильно:)