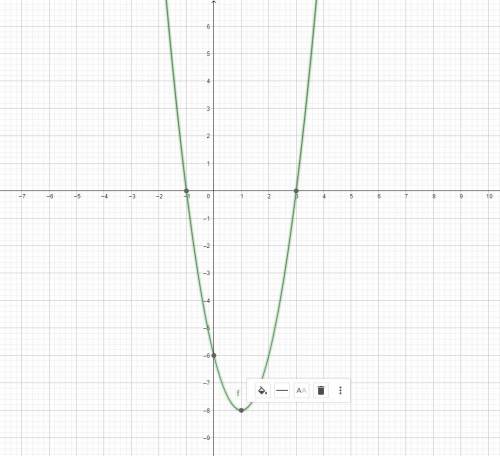
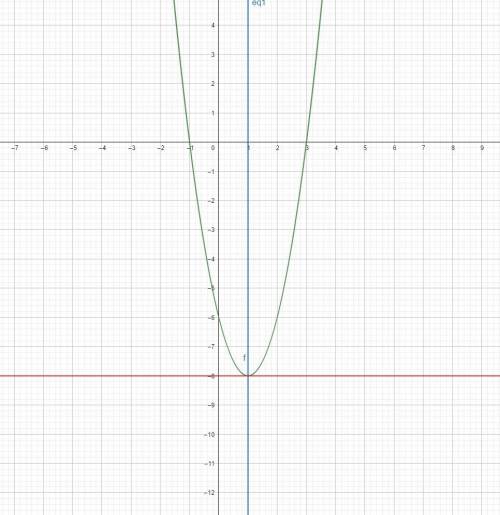
Я прикрепил фото того, как выглядит график. А сейчас разберемся как его строить.
Для начала давай раскроем скобки:
y = (2x - 6)(x + 1) //внесли двойку
y = x*(2x - 6) + (2x - 6) //раскрыли вторую скобку
y = 2x^2 - 6x + 2x - 6
y = 2x^2 - 4x - 6
Теперь можно решать по разному. Если хочешь напишу ещё
А пока воспользуемся самым действенным
Примем x0 и y0 за координаты вершины параболы.
Тогд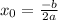а 
, а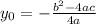 
(вторую формулу если что можно не запоминать, можешь просто подставить в уравнение полученное x0)
И так
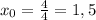
Значит
Теперь может просто подставлять значения. Но в данном случае можешь схитрить.
Так как изначальное уравнение выглядело как y = 2(x - 3)(x + 1), то если присмотреться, то можно заметить, что эта парабола пересекает ось x в точках 3 и -1. Но самое интересное это коэффициент 2. Ты можешь просто квадраты x умножать на два и получать желанную точку. После просмотра второй картинки, мои слова станут более понятны
ответ: 48см²
Объяснение: пусть одна сторона =х, а другая=у. Если 2 соседние стороны составляют в сумме 14см, то две другие, точно также будут 14 см. У нас есть первое уравнение: 2х+2у=14×2. Диагональ прямоугольника делит его на 2 равных прямоугольных треугольника в котором диагональ является гипотенузой. Составим уравнение используя теорему Пифагора: х²+у²=10². У нас есть 2 уравнения для системы:
{2х+2у=14×2 |÷2
{х²+у²=10²
{х+у=14
{х²+у²=100
{х=14-у
{х²+у²=100
Теперь подставим значение х во второе уравнение: х²+у²=100:
(14-у)²+у²=100
196-28у+у²+у²-100=0
2у²-28у+96=0
у²-14у+48=0
D=196-4×48=4
y1=(14-2)÷2=12÷2=6
y2=(14+2)÷2=16÷2=8. Итак:
у1=6; у2=8. Теперь подставим каждое значение у в уравнение: х=14-у:
х1=14-6=8
х2=14-8=6. Нам подходят оба варианта х и у, и стороны в любом случае получаются одинаковые: 6см и 8см. Теперь найдём площадь прямоугольника зная его стороны:
S=6×8=48см²
15х²у - 5ху=5xy(3x-1)
ответ: 5xy(3x-1)