1) (0; 5) ;
2) ( 4; 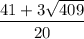 )
)
3) [ - 3; - 1) ∪ ( -1; 4]
Объяснение:
Решить неравенства
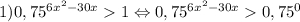
Так как основание степени 0<0,75 <1 , то показательная функция 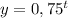 убывающая.
убывающая.
Тогда получим
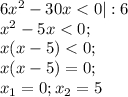
Определим знак ( во вложении) и получим
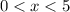 , то есть х ∈ (0; 5).
, то есть х ∈ (0; 5).
ответ : 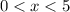
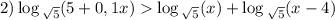
Так как логарифм определен на множестве положительных чисел, то найдем ОДЗ неравенства
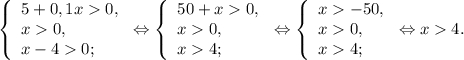
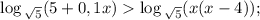
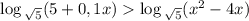
Так как 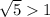 , то логарифмическая функция
, то логарифмическая функция 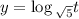 возрастающая .
возрастающая .
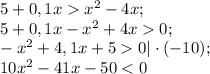
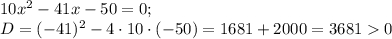
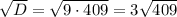
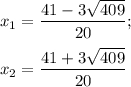
Определим знак ( во вложении)
Тогда
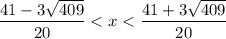
Учтем ОДЗ и получим
Так как 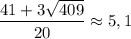 , то
, то 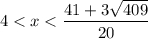
ответ: 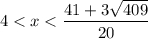
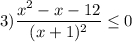
Разложим числитель на множители. Для этого решим квадратное уравнение
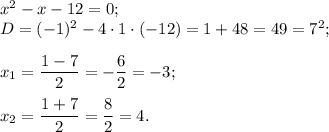
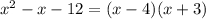
Тогда неравенство принимает вид:
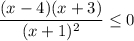
Решим неравенство методом интервалов .
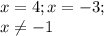
Определим знак ( во вложении)
Тогда получим
х ∈ [ - 3; - 1) ∪ ( -1; 4]



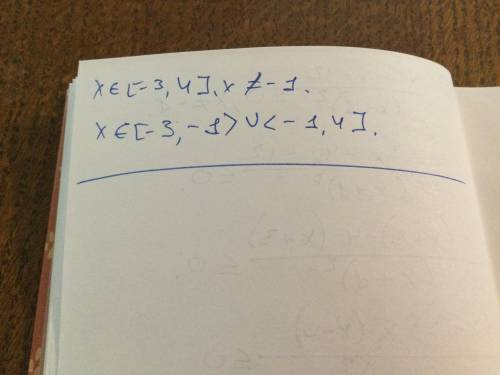
Тут все ответы расположены в правильной подстановке. Нужно только решение записать.
1) Дано: а₁ = 5, d = 3 ⠀Найти: а₇ - ?⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀РешениеФормула n - го члена арифметической прогрессии: aₙ = a₁ + d(n-1).⠀⠀⠀а₇ = 5 + 3(7-1)
⠀⠀⠀a₇ = 5 + 3*6
⠀⠀⠀a₇ = 23 – ответ
2) Дано: а₄ = 11, d = -2 ⠀Найти: а₁ - ?⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀РешениеИз формулы n-го члена найдем первый член(а₁).⠀⠀⠀aₙ = a₁ + d(n-1)
⠀⠀⠀а₄ = а₁ - 2(4-1)
⠀⠀⠀11 = а₁ - 6
Переменные перенесем в левую часть, слагаемые в правую, с противоположным знаком.⠀⠀⠀-а₁ = -6-11
⠀⠀⠀-а₁ = -17
⠀⠀⠀а₁ = 17 – ответ
3) Дано: а₄ = 12,5 , а₆ = 17,5 ⠀Найти: а₅ - ?⠀⠀⠀⠀⠀⠀⠀⠀⠀РешениеИспользуем характеристическое свойство арифметической прогрессии:⠀⠀⠀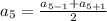
⠀⠀⠀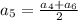
⠀⠀⠀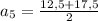
⠀⠀⠀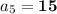 – ответ
– ответ
4) Дано: а₁ = -3, а₂ = 4 ⠀Найти: а₁₆ - ?⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение Сперва найдем разность(d) нашей прогрессии.⠀⠀⠀d = a₂ - a₁
⠀⠀⠀d = 4-(-3)
⠀⠀⠀d = 7
Теперь найдем а₁₆, использую формулу n - го члена.⠀⠀⠀а₁₆ = -3 + 7(16-1)
⠀⠀⠀а₁₆ = -3 + 7*15
⠀⠀⠀а₁₆ = -3 + 105
⠀⠀⠀а₁₆ = 102 – ответ
5) Дано: а₁ = 4, а₇ = -8 ⠀Найти: d - ?⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀РешениеОпять же используя формулу n - го члена найдем разность(d).⠀⠀⠀aₙ = a₁ + d(n-1)
⠀⠀⠀a₇ = 4 + d(7-1)
⠀⠀⠀-8 = 4 + 6d
Переменные перенесем в правую часть, слагаемые в левую, с противоположным знаком.⠀⠀⠀-6d = 4 + 8
⠀⠀⠀-6d = 12
⠀⠀⠀d =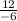
⠀⠀⠀d = -2 – ответ
6) Дано: а₇ = -5, а₃₂ = 70 ⠀Найти: а₁ - ?⠀⠀⠀⠀⠀⠀⠀⠀⠀РешениеНайдем разность, используя эту формулу:⠀⠀⠀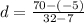
⠀⠀⠀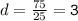
Теперь найдем первый член(а1) прогрессии опять же, с формулы n - го члена.⠀⠀⠀а₇ = а₁ + 3(7-1)
⠀⠀⠀-5 = а₁ + 3*6
⠀⠀⠀-5 = а₁ + 18
Переменные перенесем в левую часть, слагаемые в правую, с противоположным знаком.⠀⠀⠀-а₁ = 18+5
⠀⠀⠀-а₁ = 23
⠀⠀⠀а₁ = -23 – ответ
7) Дано: а₁ = 2, а₂ = 5, а₃ = 8 ⠀Найти: S₁₁ - ?⠀⠀⠀⠀⠀⠀⠀⠀⠀РешениеНам понадобится разность(d) прогрессии.⠀⠀⠀d = a₂ - a₁
⠀⠀⠀d = 5 - 2
⠀⠀⠀d = 3
Формула суммы n первых членов арифметической прогрессии:⠀⠀⠀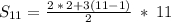
⠀⠀⠀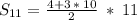
⠀⠀⠀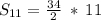
⠀⠀⠀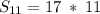
⠀⠀⠀ – ответ
– ответ