7 м
Объяснение:
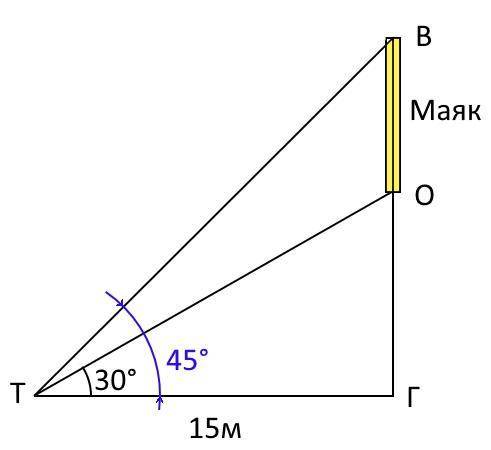
Турист находится в точке "Т" (см приложение) и наблюдает основание маяка, расположенного в точке "О", а также вершину маяка, расположенную в точке "В". Точка "Г" - это горизонт, проведенный от туриста до проекции основания маяка.
Треугольники ТГО и ТГВ прямоугольные с прямым углом в точке "Г".
Длина катета прямоугольного треугольника равна длине второго катета умноженного на тангенс противолежащего угла.
ГВ = ТГ * tg(45°) = 15 * 1 = 15 м
ГО = ТГ * tg(30°) = 15 * (√3 / 3) = 5 * 1.7 = 8.5 м
Высота маяка равна:
ГВ - ГО = 15 - 8.5 = 6.5 м
Округлив получаем 7 м
Это решение, если углы указаны в градусах. Почему то в вопросе после 30 стоит знак "секунды"...
В решении.
Объяснение:
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
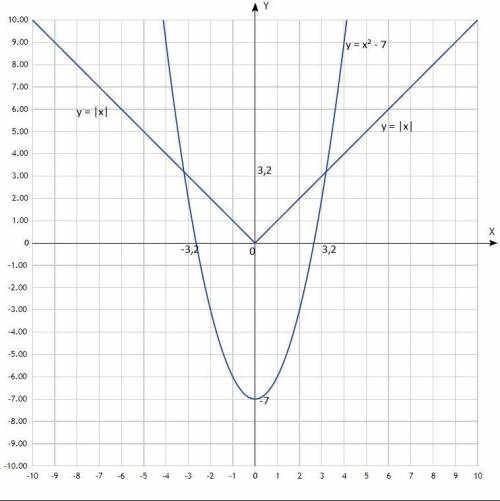
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).
(8cos^2x-4)*sqrt(3*sinx)=0
Произведение двух множителей равно нулю, если один из множителей равень нулю.
Приравниваем каждый из множителей к нулю
8cos^2x-4=0 (1)
sqrt(3*sinx)=0 (2)
Решаем отдельно, каждое из получившихся равенст
1) 8cos^2x-4=0
Переносим -4 в правую часть уравнения
8cos^2x=4
Делим обе части уравнения на 8 (т.к 8cos^2)
8cos^2x=4|:8
Решаем квадратное уравнение
cos^2x=1/2
cosx1=sqrt2/2
cosx2=-sqrt2/2
x1=+-arccos(sqrt2/2)+2pin, n~Z (значение sqrt2/2 из таблицы = pi/4)
x1=+-pi/4+2pin, n~Z
x2=+-(pi-pi/4)+2pin, n~Z
x2=-+3pi/4+2pin, n~Z
2)sqrt(3*sinx)=0
sinx=0
x=pin,n~Z
ответ: x=+-pi/4+2pin, n~Z
x=-+3pi/4+2pin, n~Z
x=pin,n~Z