(5х-3)²+(12х+5)²≤(7-13х)²+34х²+17х+410 25х²-30х+9+144х²+120х+25≤49-182х+169х²+34х²+17х+410 169х²+90х+34≤ 203х²-165х+459 169х²-203х²+90х+165х+34-459 ≤ 0 -34х²+255х-425≤0 ( : -17) 2х²-15х+25≥0 D=225-200=25=(5)² x1=(15+5)/4=5 х2=5/2=2,5 2(х-5)(х-2,5)≥0 (:2) (х-5)(х-2,5)≥0 2,55 х + - + нас интересуют только те точки ,где функция принимает положительное значение - это промежутки от -∞ до 2,5 и от 5 до +∞ точки 2,5 и 5 тоже входят , так как неравенство не строгое тогда запишем : х∈(-∞;2,5]U[5;+∞)
Формулы геометрической прогрессии * bn=b1qn−1 - формула n-го члена геометрической прогрессии. * bn=bkqn−k - формула n-го члена геометрической прогрессии через k-й член прогрессии. * b2n=bn−1bn+1 - характеристическое свойство геометрической прогрессии для трех последовательных чисел. * bnbm=bkbl - характеристическое свойство геометрической прогрессии для четырех чисел, если n + m = k + l Формулы суммы первых n членов геометрической прогрессии * Sn=q−1bnq−b1 * Sn=q−1b1(qn−1) Формула суммы бесконечной геометрической прогрессии * S=b11−qq1
1)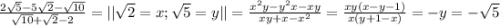
2)