а) (3/sinx)-(1/sin^2x)=2 sinx не равно 0
(3sinx-1)/Sin^2x=2 X не равно пm, где m - целое число
3sinx-1=2sin^2x
2sin^2x-3sinx+1=0
sinx=t
2t^2-3t+1=0
D=9-8=1
t1=1 t2=1/2
sinx=1 sinx=1/2
x1=п/2+2пk x2=п/6+2пn
где k - целое число x3=5п/6+2пl
где n, l - целые числа
б) x1=3п/2
x2=-11п/6
x3=-7п/6
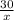часов.
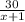часов. Первый турист пришёл в город на 1 час раньше. 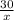- 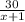= 1 (умножим на х(х+1), чтобы избавиться от дробей).
- 
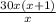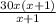= 1
= 
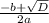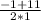= 5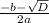
= 
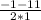= -6 х<0 - не подходит.
Найдем производную
Найдем нуль производной
х = 1,5
проверяем знаки производной на получившихся промежутках
от минус бесконечности до 1,5 имеет знак "-" от 1,5 до бесконечности "+", учитывая ОДЗ
Область допустимых значений функции
2х-1>0
2x>1
x>0.5
ответ (0,5; 1,5) убывает