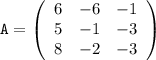
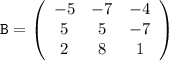
---------------------------------
---------------------------------
c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁ + a₁₃ · b₃₁ = 6 · (-5) + (-6) · 5 + (-1) · 2 = (-30) - 30 - 2 = -62
c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂ + a₁₃ · b₃₂ = 6 · (-7) + (-6) · 5 + (-1) · 8 = (-42) - 30 - 8 = -80
c₁₃ = a₁₁ · b₁₃ + a₁₂ · b₂₃ + a₁₃ · b₃₃ = 6 · (-4) + (-6) · (-7) + (-1) · 1 = (-24) + 42 - 1 = 17
c₂₁ = a₂₁ · b₁₁ + a₂₂ · b₂₁ + a₂₃ · b₃₁ = 5 · (-5) + (-1) · 5 + (-3) · 2 = (-25) - 5 - 6 = -36
c₂₂ = a₂₁ · b₁₂ + a₂₂ · b₂₂ + a₂₃ · b₃₂ = 5 · (-7) + (-1) · 5 + (-3) · 8 = (-35) - 5 - 24 = -64
c₂₃ = a₂₁ · b₁₃ + a₂₂ · b₂₃ + a₂₃ · b₃₃ = 5 · (-4) + (-1) · (-7) + (-3) · 1 = (-20) + 7 - 3 = -16
c₃₁ = a₃₁ · b₁₁ + a₃₂ · b₂₁ + a₃₃ · b₃₁ = 8 · (-5) + (-2) · 5 + (-3) · 2 = (-40) - 10 - 6 = -56
c₃₂ = a₃₁ · b₁₂ + a₃₂ · b₂₂ + a₃₃ · b₃₂ = 8 · (-7) + (-2) · 5 + (-3) · 8 = (-56) - 10 - 24 = -90
c₃₃ = a₃₁ · b₁₃ + a₃₂ · b₂₃ + a₃₃ · b₃₃ = 8 · (-4) + (-2) · (-7) + (-3) · 1 = (-32) + 14 - 3 = -21
---------------------------------
----------------------------------------
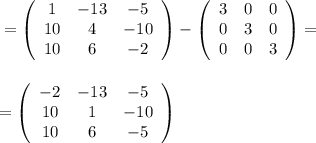
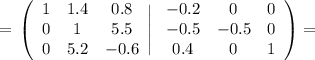
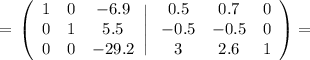
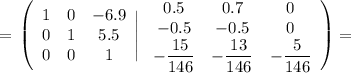
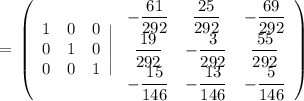
Объяснение:
Дано неравенство:
По свойству логарифма, мы знаем, что аргумент логарифма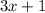
всегда должен быть больше нуля. Поэтому найдём область допустимых значений неравенства:
Теперь найдем множество решений нашего неравенства в виде системы с областью допустимых значений. Представим число 2 как логарифм с аргументом 5 по основанию 5:
Для выражения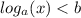
при 
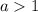равно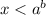 
, поэтому наше неравенство имеем право представить в виде:
Преобразуем:
Исходя из области допустимых значений и множества решений самого неравенства, получаем пересечение: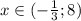
или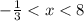 
.