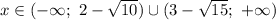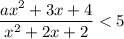
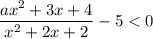
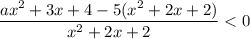
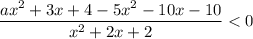
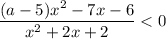
Неравенство вида 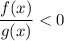 равносильно двум системам неравенств:
равносильно двум системам неравенств:
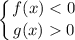 и
и 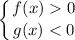
Тогда имеем две системы неравенств:
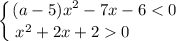 и
и 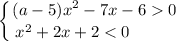
Рассмотрим первую систему неравенств:
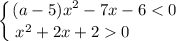
Решим второе неравенство системы:
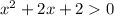
Пересечение с осью абсцисс:
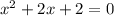
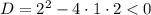
Дискриминант отрицательный, значит график квадратичной функции 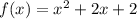 находится над осью абсцисс и при любых
находится над осью абсцисс и при любых  больше нуля.
больше нуля.
Тогда решением неравенства будет 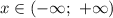
Рассмотрим первое неравенство системы:
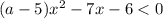
Поскольку следует найти значения параметра  , при которых
, при которых 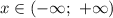 , то для решения системы неравенств нужно, чтобы и данное неравенство имело решение
, то для решения системы неравенств нужно, чтобы и данное неравенство имело решение 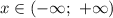
Если 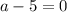 , то есть
, то есть 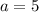 , то имеем линейное неравенство:
, то имеем линейное неравенство:

Решением данного неравенства будет 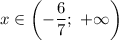 , что не удовлетворяет условию задачи.
, что не удовлетворяет условию задачи.
Тогда при 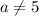 решим неравенство.
решим неравенство.
Если 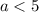 , то имеем параболу с ветвями, направленными вниз, если
, то имеем параболу с ветвями, направленными вниз, если 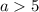 , то имеем параболу с ветвями, направленными вверх.
, то имеем параболу с ветвями, направленными вверх.
Пересечение с осью абсцисс:
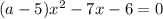
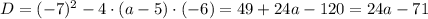
Если 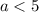 , то данное неравенство будет иметь решение
, то данное неравенство будет иметь решение 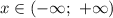 , если
, если 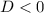 , то есть если
, то есть если  или
или 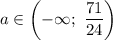
Если 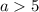 , то данное неравенство не может иметь решение
, то данное неравенство не может иметь решение 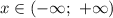
Таким образом, если 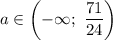 имеем решение
имеем решение 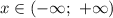
Рассмотрим вторую систему неравенств:
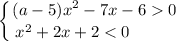
Решим второе неравенство системы:
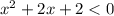
Пересечение с осью абсцисс:
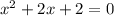
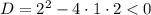
Если дискриминант отрицательный, то квадратичная функция 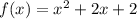 никогда не будет меньше нуля.
никогда не будет меньше нуля.
Тогда решением неравенства будет 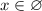
Тогда общим решением системы неравенств будет 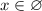 , независимо от значений параметра
, независимо от значений параметра 
ответ: 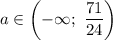
Преобразуем второй модуль и определим нули подмодульных выражений:
Нули подмодульных выражений: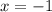 и
и  , поэтому раскрывать модуль будем на следующих промежутках:
, поэтому раскрывать модуль будем на следующих промежутках:
1)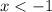
2)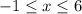
3)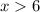
1) Раскрываем модуль на промежутке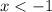 . Первый модуль раскрывается со сменой знака, второй - без смены знака:
. Первый модуль раскрывается со сменой знака, второй - без смены знака:
Найдем корни соответствующего уравнения:
Методом интервалов найдем решение неравенства:
Учтем условие раскрытия модуля. Для этого сравним числа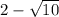 и
и 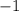 :
:
Значит, первое число меньше. Тогда, учитывая условие раскрытия модуля, получим:
2) Раскрываем модуль на промежутке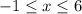 . Оба модуля раскрываются со сменой знака:
. Оба модуля раскрываются со сменой знака:
Методом интервалов найдем решение неравенства:
Учтем условие раскрытия модуля. Сравним числа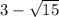 и
и 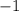 :
:
Первое число больше.
Сравним числа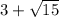 и
и 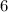 :
:
Первое число больше.
Теперь, учитывая условие раскрытия модуля, получим:
3) Раскрываем модуль на промежутке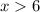 . Оба модуля раскрываются без смены знака:
. Оба модуля раскрываются без смены знака:
Используя метод интервалов, запишем решение неравенства:
Число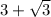 меньше числа
меньше числа 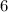 .
.
Запишем решение, учитывая условие раскрытия модуля:
Итоговое решение неравенства представляет собой объединений трех промежутков:
Упростив запись, получим:
ответ: