1-Г, 2-Г, 3-В
Объяснение:
1. График пересекает ось ординат, когда Х=0. Подставим Х=0 в функции:
а) у(0)=3⁰+1=2 => график функции пересекает ось ОУ
б) у(0)=tg0=0 => график функции пересекает ось ОУ
в) у(0)=(0-2)²=4 => график функции пересекает ось ОУ
г) у(0)=log3 (0-2)=log3(-2) - график функции не пересекает ось ОУ, т.к. у(0) не существует.
ответ: Г.
2. Подставим число 3 во все уравнения:
а) х²=-9, 3²=-9, 9=-9 - неверно
б) √х+13=-4, √3+13=-4, √16=-4, 4=-4 - неверно
в) 3^х=1, 3³=1, 27=1 - неверно
г) logx(9)=2, log3(9)=2 - верно
ответ: Г.
3. (1+√8)²-4√2=1+2√8+8-4√2=9+4√2-4√2=9
ответ: В.
Вроде так
1) f'(x)=(sin²x)'=2*sinx*cosx=sin2x; f''(x)=(sin2x)'=2cos2x;
2)f'(x)=(cos2x)'=-2*sin2x; f''(x)=(-2sin2x)'=-4cos2x
3) f'(x)=(√x)'=1/(2√x)=(x⁻¹/²)/2; f''(x)=((x⁻¹/²)/2)'=-(1/4)*x⁻³/²=-1/(4x√x)
4) f'(x)=(x²-2√x)'=2x-(2/(2√x))=(2x-x⁻¹/²); f''(x)=(2x-(x⁻¹/²))'=2-(-1/2)*x⁻³/²=
2+1/(2x√x);
5) f'(x)= (xsinx)'=sinx+x*cosx; f''(x)=сosx+cosx-x*sinx=2cosx-x*sinx;
6) f'(x)=(xcos3x)'=cos3x-3x*sin3x; f''(x)=(cos3x-3x*sin3x)'=-3sin3x-3sin3x-9x*сos3x=-6sin3x-9x*сos3x;
7) f'(x)=(3x²-cos(x²+1))'=6x+sin(x²+1)*(2x)=2x*(3+sin(x²+1)); f''(x)=
(2x*(3+sin(x²+1)))'=
2*(3+sin(x²+1))+2x*(2x*cos(x²+1))=6+2sin(x²+1)+4x²*cos(x²+1);
8) f'(x)=(sin²2x)'=2*sin2x*(cos2x)*2=2sin4x; f''(x)=(2sin4x)'=8*cos4x;
9) f'(x)=(x²sin2x)'=2x*sin2x+2x²*cos2x;
f''(x)=(2x*sin2x+2x²*cos2x)'=2*sin2x+4x*cos2x+4x*cos2x-4x²*sin2x=
2*sin2x+8x*cos2x-4x²*sin2x
Формула преобразования тригонометрического выражения
Вс аргумент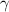
определяется из условий
=====================================================
ответ: область значений y ∈ [-5; 5]