Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
Объяснение:
y = - x⁴ + 8x² - 16
y' = - 4x³ + 16x
y' = 0
- 4x³ + 16x = 0
4x(x² - 4) = 0
x = 0, x² - 4 = 0
(x - 2)(x + 2) = 0
x = 2 x = - 2
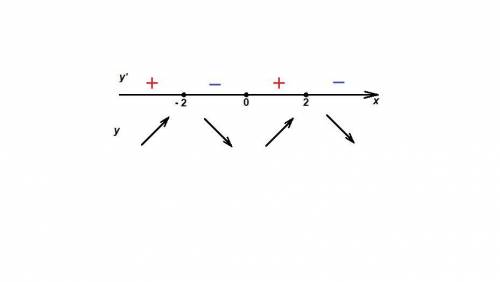
Отметим точки на координатной прямой и определим знаки производной на получившихся интервалах (знаки чередуются, справа минус), см. рисунок.
Если на промежутке производная положительна, то функция возрастает, если отрицательна - убывает.
Функция убывает при x ∈ [- 2; 0] ; [2; + ∞).
Функция возрастает при x ∈ (- ∞; - 2] ; [0; 2].
Обозначим собственную скорость моторной лодки за (х) км/час, тогда скорость лодки по течению равна:
(х+2) км/час, а против течения реки, скорость лодки равна:
(х-2) км/час)
Расстояние 60 км лодка проплыла за время:
60/(х+2) час, а расстояние 32 км, лодка проплыла за время:
32/(х-2) час
А так как общее время в пути составило 5 часов, то:
60/(х+2)+32/(х-2)=5
(х-2)*60+(х+2)*32=(х+2)*(х-2)*5
60х-120+32х+64=5х²-20
5х²-20-92х+56=0
5х²-92х+36=0
х1,2=(92+-D)/2*5
D=√(8464-4*5*36)=√(8464-720)=√7744=88
х1,2=(92+-88)/10
х1=(92+88)/10
х1=18
х2=(92-88)/10
х2=0,4 - не соответствует условию задачи- низкий показатель для скорости моторной лодки
Отсюда:
Собственная скорость моторной лодки 18км/час