Функция у = f(x) имеет:
область определения - множество всех допустимых значений переменной х (обозначают D(у);
множество значений - множество соответствующих значений переменной у (если подставлять вместо х возможные числа, будут получаться значения переменной у, т. е. зависящие от значений х значения переменной у - они и образуют множество значений функции) - обозначают Е(у).
Пример. Найти область определения и множество значений функции у = х² + 3.
D(у) = R (т.е. множество всех действительных чисел), тогда т.к. х² ≥ 0 для всех возможных значений х, то х² + 3 ≥ 3, а, следовательно, множество значений данной функции Е(у) = [3; +∞).
ответ: D(у) = R, Е(у) = [3; +∞).
x² + 2x + 3 = 0
D = 2² - 4 * 3 = 4 - 12 = - 8 < 0
Дискриминант меньше нуля старший коэффициент больше нуля, значит x² + 2x + 3 > 0 при любых действительных значениях x .
Следовательно можно разделить обе части на это положительное число и знак неравенства не изменится.
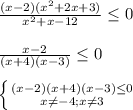
- + - +
________₀___________[2]___________₀__________
- 4 3
ответ : x ∈ ( - ∞ ; - 4) ∪ [2 ; 3)
ответ 2 м
Объяснение:
пусть сарафан - х , тогда платье - у
у + 3х = 9м
3у + 5х = 19м решаем систему
3(9 - 3х) + 5х = 19 м
27 - 9х + 5х = 19
-4х = -8
х=2 (м)