1 - 150 (1)
2 - 210 (2)
3 - 168 (3)
Объяснение:
Решение через проценты:
Представим что первая типография выпустила 100% книг, значит вторая выпустит на 40% больше, т.е. 140%Если 140% выпустила вторая типография, то третья типография выпустит 140% · 4/5 = 112% Суммируем проценты и находим один процент от общего кол-ва книг: 100 + 140 + 112 = 352; 528:352 = 1.5 Первая типография: 100 · 1.5 = 150 (1); Вторая типография: 140 · 1.5 = 210 (2); Третья типография: 112 · 1.5 = 168 (3);Что-бы убедиться в правильности решения, можем найти их сумму:
150+210+168 = 528
Решение через части:
Первая типография:
Вторая типография: 
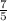Третья типография: · 
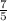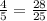Сумма: 
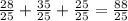Найдем 1/25 часть 
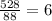Первая типография: 25 * 6 = 150 (1); Вторая типография: 25 * 35 = 210 (2); Третья типография: 25 * 28 = 168 (3);
1 - 150 (1)
2 - 210 (2)
3 - 168 (3)
Объяснение:
Решение через проценты:
Представим что первая типография выпустила 100% книг, значит вторая выпустит на 40% больше, т.е. 140%Если 140% выпустила вторая типография, то третья типография выпустит 140% · 4/5 = 112% Суммируем проценты и находим один процент от общего кол-ва книг: 100 + 140 + 112 = 352; 528:352 = 1.5 Первая типография: 100 · 1.5 = 150 (1); Вторая типография: 140 · 1.5 = 210 (2); Третья типография: 112 · 1.5 = 168 (3);Что-бы убедиться в правильности решения, можем найти их сумму:
150+210+168 = 528
Решение через части:
Первая типография:Вторая типография: 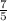Третья типография: 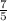· 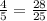Сумма: 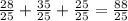Найдем 1/25 часть 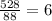Первая типография: 25 * 6 = 150 (1); Вторая типография: 25 * 35 = 210 (2); Третья типография: 25 * 28 = 168 (3);
решить уравнение
sin2x- 3√(sinx)=0 ⇔2sinxcosx - 3√(sinx)=0 ⇔2√(sinx)*(cosx*√(sinx) - 1,5)=0
а) √(sinx) = 0 ⇔sinx =0 ⇔ x =πn , n ∈ ℤ .
б) cosx*√(sinx) -1,5 =0 ⇔ cosx*√(sinx) = 1, 5 ⇒ x∈ ∅
ответ: x =πn , n ∈ ℤ .
* * * * * * * Если * * * * * * * * * * * * *
sin²x- 3√(sinx)=0 ⇔√sinx*(√sin³x - 3)=0
а) √(sinx) = 0 ⇔sinx =0 ⇔ x =πn , n ∈ ℤ .
б) √sin³x - 3=0 ⇔ √sin³x = 3 ⇒ x∈ ∅