Якщо число x є розв'язком як нерівності x>−4, так і нерівності х<5, тоді воно є розв'язком подвійної нерівності −4<x<5.
Множину усіх чисел, що задовільняють подвійній нерівності −4<x<5 називають числовим проміжком і позначають: (−4;5).
Зобразимо проміжок на малюнку. Точки малюємо виколотими, оскільки вони не належать проміжку.
51_t02(1).png
Розглянемо інші проміжки.
−4≤x≤5 або x∈[−4;5]. Читається: «Проміжок від −4 до 5, включаючи −4 та 5».
51_t02(4).png
−4≤x<5 або x∈[−4;5). Читається: «Проміжок від −4 до 5, включаючи −4».
51_t02(2).png
−4<x≤5 або x∈(−4;5]. Читається: «Проміжок від −4 до 5, включаючи 5».
51_t02(3).png
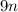
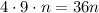
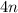
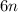

![[4,6]=2\cdot 2\cdot 3=12](/tpl/images/0629/9227/9a182.png)
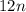
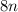
так как y = x - 1
то мы подставляем это в первое уравнение
х(2) + 2 (х-1) = 6
Х(2) + 2х - 2 = 6
х(2) +2х = 8
приравниваем к 0
x(2) + 2x -8 =0
дискриминант = 2*2- 4 *(-8) *1 = 4 + 32 = 36
x1 = -4
x2= 2
подставляем иксы во второй уравнение
y1 = -4 - 1 = -5
y2 = 2- 1 = 1