Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 6, 12, 14 и 8, тогда получим четыре числа, которые образуют арифметическую прогрессию. Найди числа, которые образуют геометрическую прогрессию.
знаменатель геометрической прогрессии: q= 2
члены геометрической прогрессии :
b1= 4
b2=8
b3= 16
b4=32
Решение
b₁; b₁·q; b₁·q²; b₁·q³ геометрическая прогрессия
тогда
b₁+6; b₁·q+12; b₁·q; b₁·q³ арифметическая прогрессия
по характеристическому свойству арифметической прогрессии
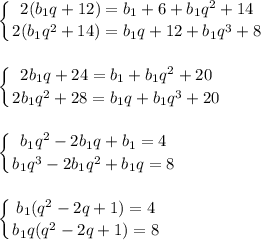
q ≠ 1
разделим второе уравнение на первое
q = 2
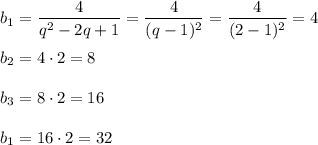
20 км/ч.
Объяснение:
Для решения этой задачи нужно составить уравнение, а уравнение содержит в себе две равные части.
За х я взял скорость лодки.
Получается, что скорость катера по течением реки равна х + 5км/ч,
а против течения х - 5км/ч.
Для уравнения нужно использовать 1% от всего пути по реке.
Это значит, что нужно его найти от каждого проделанного пути по и против течения реки.
1% всего пути лодки против течения:
(х - 5кмп/ч. * 2ч) : 24%.
Для того чтобы узнать 1% от пути нужно узнать сначала путь формулой V * T = S, и потом делить на проценты проделанного пути против течения в соотношении с проделанным путем по течению.
Получается одна двенадцатая икс минус пять двенадцатых.
Точно также со 1% по течению.
А так как эти проценты относятся к одному целому можно составить такое уравнение:
Одна двадцатая икс плюс одна четвертая равно одна двенадцатая икс минус пять двенадцатых.
Его корень - 20.
Х - скорость лодки в стоящей воде.
Объяснение:сщяс решу