При каких значениях "а" система \left \{ {{x^{2}+y^{2}+2xy-6x-6y+10=a} \atop {x^{2}+y^{2}-2xy-2x+2y+a=0 }} \right.\\ имеет одно решение? Найти эти решения при найденных "а".
Значения высоты, на которую отскакивает шар, составляют убывающую геометрическую прогрессию с .
Сумма вертикальных расстояний, пройденных мячом вниз - это сумма всех членов убывающей прогрессии
метров.
Сумма вертикальных расстояний, пройденных мячом вверх - это сумма всех членов убывающей прогрессии за вычетом первого члена (т.к. на 3 м вниз мяч пролете только вниз)
м.
Тогда сумма вертикальных расстояний пройденных мячом вниз и вверх
метров метров.
P.S. Можно рассмотреть расстояния, пройденные вниз как г.п. с , а расстояния, пройденные вверх как г.п. с и найти сумму каждой г.п. ответ будет тем же.
да тут приравнять функции, решить получившееся, найти х а потом и у 1)х²=-х х²+х=0 х(х+1)= ⇒х1=0; x2=-1 ⇒y1=0; y2=1 ответ (0,0) (-1.1) 2) -x²=x -x²-x=0 -x(x+1)=0 ⇒ x1=0; x2=-1; ⇒y1=0; y2= 1 ответ (0,0) (-1.1) 3) x²=-x+6 x²+x-6=0 d=1+24=25 ⇒ x1=(-1-5)/2=-3 y1=9 x2=(-1+5)\2=2 ⇒y2=4 ответ (-3,9) (2,4) 4)-x²=2x-3 -x²-2x+3=0 d=4+12=16 ⇒x1=(2-4)\-2=1 y1=-1 x2=(2+4)\-2=-3 y2=-9 ответ (1,-1) (-3,-9) 5) x-2=2x-3-x=-1x=1 y=-1ответ (1,-1)6) x²= x-3x²-x+3=0 d=1-12=-11 решений нет, то есть функции не пересекаются
Значения высоты, на которую отскакивает шар, составляют убывающую геометрическую прогрессию с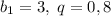
.
Сумма вертикальных расстояний, пройденных мячом вниз - это сумма всех членов убывающей прогрессии
Сумма вертикальных расстояний, пройденных мячом вверх - это сумма всех членов убывающей прогрессии за вычетом первого члена (т.к. на 3 м вниз мяч пролете только вниз)
Тогда сумма вертикальных расстояний пройденных мячом вниз и вверх
P.S. Можно рассмотреть расстояния, пройденные вниз как г.п. с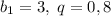
, а расстояния, пройденные вверх как г.п. с 
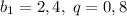и найти сумму каждой г.п. ответ будет тем же.