АЛГЕБРА ЕСЛИ ЧТО СДЕЛАЙТЕ НА ЛИСТОЧКЕ.
ЗАДАНИЕ
прочитать,разбирая каждый пример №588, 590 (1 .выделяем две функции,одна в левой части уравнения другая в правой, 2. для каждой заполняем таблицу, 3. чертим два графика в одной системе координат, 4. находим абсциссы! точек пересечения графиков и пишем ответ).
 км/мин.
км/мин.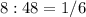 км/мин.
км/мин.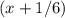 км/мин.
км/мин.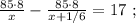
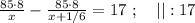
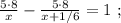
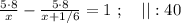
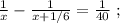
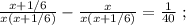
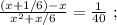
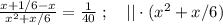
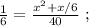
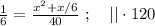
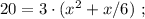
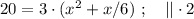
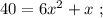
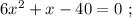
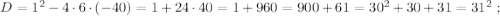
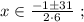
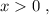 так, как это скорость,
так, как это скорость,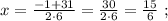
Пусть скорость медленного гонщика составляет
Раз быстрый гонщик обогнал впервые медленного через 48 минут, то с таким же успехом, мы можем переформулировать это утверждение и так: быстрый гонщик через 48 минут опережал медленного на 8 км (длину одного круга). А значит, их относительная скорость удаления составляет:
Из найденного следует, что скорость быстрого гонщика мы можем записать, как:
Сказано, что медленный гонщик ехал на 17 минут дольше, а значит, если мы вычтем из времени в пути медленного гонщика время в пути быстрого гонщика, то эта разность и должна составить 17 минут. Ясно, что время в пути для каждого гонщика мы можем найти, разделив полный путь трассы на скорость каждого из них, тогда:
Поскольку
направленная в заданную сторону (вперёд), то:
Это и есть скорость второго (медленного) гонщика.
Осталось только перевести её в км/ч:
15/6 км/мин = 15 км : 6 мин = 150 км : 60 мин = 150 км : час = 150 км/час.
О т в е т : 150 км.