ответ: Первый кран наполнит пустую ванну за 18 минут; второй кран опорожнит полную ванну за 12 минут.
Пошаговое объяснение: Пусть вся ванна 1 (единица), а х минут это время за которое первый кран наполнит ванну, тогда время за которое второй кран опорожнит ванну, будет х-6 минут. Производительность первого крана на наполнение будет 1/х; производительность второго крана на опорожнение будет 1/(х-6) , а совместная производительность на опорожнение ванны 1/36. Составим уравнение:
1/(х-6) - 1/х = 1/36
36х-36(х-6)=х(х-6)
х²-6х-216=0
D=900
х₁=-12 (мин) не подходит, т.к. время не может быть отрицательным.
х₂=18 (мин) время за которое первый кран наполнит пустую ванну.
18-6=12 (мин) время за которое второй кран опорожнит полную ванну.
Объяснение:

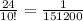

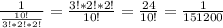
Могу пока что только первые два, т.к листочка нет сейчас...
1) вершина параболы ищется по формуле X(0)=-b/2a
b=-6 (b это коэффициент при X)
a=1 (a это коэффициент при X квадрат)
значит X(0)=6/2=3 (это абсцисса вершины (Если не знаешь что это, то это величина по оси X)
теперь считаем Y(0) (или ординату вершины)
Y(0) считается подстановкой X(0) в уравнение.
Y(0)=3^2-6*3+4=9-18+4=-5
Следовательно координата вершины (3;-5)
2) Точки пересечения с осями координат, это точки, в которых график пересекается с Осью Х или осью Y.
Смотри, там где парабола пересекает Ось Y, Х=0 (т.к на оси У, Х всегда равен 0)
Значит мы подставляем в эту функцию вместо Х ноль, и таким образом находим точку пересечения с Осью У.
Y=0^2-6*0+4=4
И мы получаем точку (0;4) ( Ноль это абсцисса)
Что бы найти точки пересечения с Осью Х, мы соответственно наоборот приравниваем к Нулю У.
Получаем квадратное уравнение:
x^2-6x+4=0
D=36-16=20
X(1)=(6+2√5)/2=3+√5
X(2)=(6-2√5)/2=3+√5
Итак мы получили два корня (Да, они могут быть иррациональные)
Значит точки пересечения с Осью Х две: (3+√5;0)
(3-√5;0)