В решении.
Объяснение:
d) |4 - x| < 5
Схема:
4 - x < 5; 4 - x > -5
-x < 5 - 4 -x > -5 - 4
-x < 1 -x > -9
x > -1 x < 9
(знак неравенства меняется при умножении или делении на минус).
Решение неравенства: х∈(-1; 9).
Неравенство строгое, скобки круглые.
е) |3x - 9| + 2 > 7
|3x - 9| > 7 - 2
|3x - 9| > 5
Схема:
3x - 9 > 5 3x - 9 < -5
3x > 5 + 9 3x < -5 + 9
3x > 14 3x < 4
x > 14/3 x < 4/3
Решение неравенства: (-∞; 4/3)∪(14/3; +∞).
Неравенство строгое, скобки круглые.
f) |3x + 2| - 1 >= 10
|3x + 2| >= 10 + 1
|3x + 2| >= 11
Схема:
3x + 2 >= 11 3x + 2 <= -11
3x >= 11 - 2 3x <= -11 - 2
3x >= 9 3x <= -13
x >= 3 x <= -13/3
Решение неравенства: (-∞; -13/3]∪[3; +∞).
Неравенство нестрогое, скобки квадратные, а знаки бесконечности всегда с круглой скобкой.
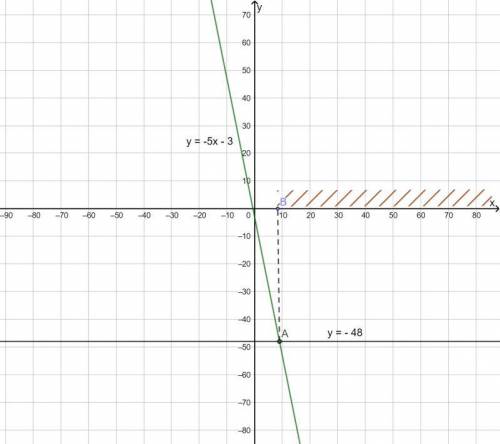
1) При x ≥ 9 значения функции y = -5x - 3 не больше -48.
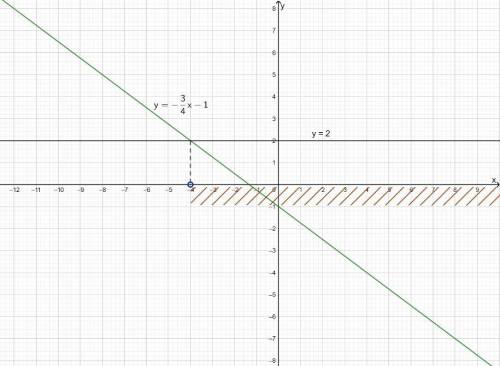
2) При x > -4 значения функции y = -3/4 *x - 1 меньше 2.
Объяснение:
Рисунки прилагаются.
1) y = -5x - 3 линейная функция, график прямая линия, пересекает ось OY в точке (0; --3).
Выберем еще одну точку и построим график функции: x = 10; y = -50-3 = -53.
При каких значениях x значения функции не больше (значит меньше или равно) -48?
Построим в этой же системе координат прямую y = -48.
По графикам видно, что что -5x - 3 ≤ -48 при x ≥ 9
Проверим аналитически:
-5x -3 ≤ -48; -5x ≤ -48 +3; -5x ≤ -45; x ≥ 9.
2) y = -3/4*x - 3 = -0,75x - 1 линейная функция, график прямая линия, пересекает ось OY в точке (0; -1).
Выберем еще одну точку и построим график функции: x = 4;
y = -0,75*4 -1 = -3 - 1 = -4.
При каких значениях x значения функции меньше 2?
Построим в этой же системе координат прямую y = 2.
По графикам видно, что -0,75x - 1 ≤ -2 при x > -4
Проверим аналитически:
-0,75x -1 < 2; -0,75x < 3; x > -4.
Вот как то так наверное)))