A) 65х-13-60х-30<0
65х-60х<13+30
5х<43
х<8,6
ответ:(-бесконечность;8,6)
Б)42-1,2х-40+2х>0
-1,2х+2х>-42+40
0,8х>-2
х>-2,5
ответ:(-2,5;+бесконечности)
25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:

Число, следующее за четвертым членом последовательности 25.
решения.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
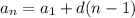
Наименьшее натуральное число делящееся на 5 это 5, т.е.  .
.
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е. 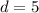 .
.
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.
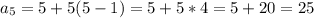
а) 13(5х-1)-15(4х+2)<0
65x-13-60x-30 <0
5x < 43
x <8.6
ответ(-бесконечность;8.6)
б 6(7-0.2Х)-5(8-0.4Х)>0
42-1.2х-40+2х > 0
0.8х > -2
х >-2.5
ответ(-2.5;+бесконечность)