a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: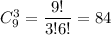 
из них нужно взять 2 синих и 1 красный карандаш, таких у нас 
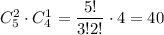. Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21
РЕШЕНИЕ
1.
Всего событий - n.
N(A) = 8 - благоприятных для А - дано.
N(B) = n - N(A) = 17 - 8 = 9 - благоприятных для В - ОТВЕТ
р(А) = 0,32 - вероятность А - дано.
р(В) = 1 - 0,32 = 0,68 - вероятность события В - ОТВЕТ
2.
Всего вариантов на кости - граней - n =6.
Событие А - выпало четное - A={2,4,6} - m(А) = 3
Событие В - больше 3 - B={4,5,6} - m(B) = 3
Событие АВ - пересечение множеств А∩В = {4;6} - m(AB) = 2.
Вероятность АВ по классической формуле
p(AB) = m(AB)/n = 2/6 = 1/3 - вероятность - ОТВЕТ (≈33,3%)
3.
Всего для каждого броска вариантов - n = 6.
Событий А - меньше 3 - A={1,2} - m(A) = 2, p(A) = 2/6 = 1/3
Событие В - больше 4 - B={5,6} - m(B) = 2, p(B) = 2/6 = 1/3
Элементарные события:
1,5 и 1,6 и 2,5 и 2,6 - четыре варианта.
Событие А*В - "И" А "И" В - произведение вероятностей каждого.
p(A*B) = 1/3 * 1/3 = 1/9 - вероятность - ОТВЕТ (≈11,1%)
ИЛИ
Для двух бросков = n = 6² = 36, m(AB) = 4, p(A*B) = 4/36 = 1/9 - ОТВЕТ
4.
Вероятность несовместных событий ("ИЛИ") равна сумме вероятностей каждого - называется "ИЛИ" U "ИЛИ" V.
Р(U+V) = р(U)+р(V) = 0,3 + 0,5 = 0,8 - вероятность - ОТВЕТ