Два фермера, работая вместе, могут вспахать поле за 25 часов.
Производительность труда у первого и второго относятся как 2:5.
Фермеры планируют работать поочередно.
Сколько времени должен проработать второй фермер, чтобы поле было вспахано за 45,5 часов?
Пусть Х-производительность 1-го, У-производительность 2-го.
Система:
х+у=125
2х=5у
Последовательно:
2х+2у=2/25
2х-5у=0
7у=2/25 и у=2175
Тогда х=135
Итак, производительности мы нашли.
Поочередно фермеры работали 45,5 часа = 91/2 часа.
Пусть из этого времени 2-ой работал Т часов, тогда 1-ый работал 912-Т часов.
Уравнение:
(91/2-Т)⋅(1/35)+Т⋅(2/175)=1
имеет корень Т=17,5
Проверка.
1. проверим , что х+у=125
1/35+2/175=(70+175)/(175⋅35)=7/175=1/25
2. проверим, что 2х=3у:
2/35=5⋅2/175
3. Проверим уравнение при поочередной работе:
Если 2-ой работал 17,5 часов, то 1-ый работал 45,5-17,5=28 часов
28⋅135+(352)⋅(2175)=28/35+1/5=1
ОТВЕТ: 17,5
48 квадратных сантиметров
Объяснение:
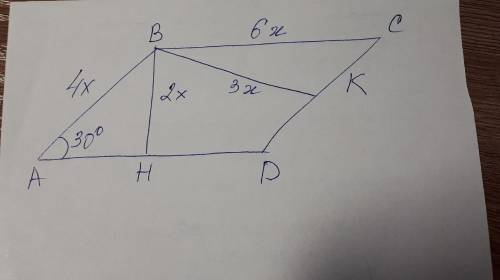
1) Примем одну высоту параллелограмма за 2х (на рисунке это сторона BH), тогда вторую высоту примем за 3х (на рисунке это сторона BK).
2) Поскольку катет против угла в 30° равен половине гипотенузы, то из треугольника АВН получаем, что гипотенуза АВ = 4х.
3) Далее рассмотрим треугольник ВСК. Получаем, что сторона ВС= 6х
4) Затем вычислим периметр параллелограмма: (4х+6х)*2=40 сантиметров
5) 20х=40, откуда х=2
6) Таким образом, можно сделать вывод, что одна сторона 4х=4·2=8 см.
7) Высота проведенная к этой стороне 3х=3·2=6 см
8) Таким образом получаем, что площадь параллелограмма равна 8*6=48 квадратных сантиметров
1)
2x - y = 2
2x^2 - xy = 6
y = 2x - 2
x(2x - y) = 6
y = 2x - 2
x(2x - 2x + 2) = 6
y = 2x - 2
2x = 6
x = 3
y = 4
ответ: x = 3; y = 4
2)
(x + 2)(y + 1) = 12
x + 2y = 6
x = 6 - 2y
(6 - 2y + 2)(y + 1) = 12
x = 6 - 2y
(8 - 2y)(y + 1) = 12
x = 6 - 2y
8y + 8 - 2y^2 - 2y - 12 = 0
x = 6 - 2y
-(2y^2 - 6y + 4) = 0
x = 6 - 2y
2(y^2 - 3y + 2) = 0
x = 6 - 2y
y^2 - 3y + 2 = 0
x = 6 - 2y
y1 = (3 + корень(9 - 8)) : 2
y2 = (3 - корень(9 - 8)) : 2
y1 = 2
y2 = 1
x1 = 2
x2 = 4
ответ: (2; 2) и (4; 1), где первое число в скобках - X, а второе y
3)
x^2 + y^2 = 10
xy = -3
Y и X неравны 0, делить можно
x^2 + y^2 = 10
x = (-3) : y
x = (-3) : y
9 : y^2 + y^2 = 10
x = (-3) : y
(9 + y^4) : y^2 = 10
x = (-3) : y
y^4 - 10y^2 + 9 = 0
x = (-3) : y
Используем метод новой переменной:
z = y^2
z^2 - 10z + 9 = 0
x = (-3) : y
z1 = (10 + корень(100 - 36)) : 2
z2 = (10 - корень(100 - 36)) : 2
X = (-3) : y
z1 = 9
z2 = 1
X = (-3) : y
y1^2 = 9
y2^2 = 1
y1 = -3
y2 = 3
y3 = -1
y4 = 1
x1 = 1
x2 = -1
x3 = 3
x4 = -3
ответ:(1; - 3) и (-1; 3) и (3; - 1) и (-3; 1), где первое число в скобках - X, а второе y