Question

Найдите точку минимума функции y=400/x+x+7

Answer 1

Решение:

Ищем точку минимума функции: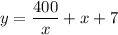 $\displaystyle y = \frac{400}{x} + x + 7$.

Для этого сначала найдем производную этой функции:

$\displaystyle y ' = \bigg (\frac{400}{x} \bigg )'+(x)'+(7)' = 400 \cdot (-1) \cdot x^{-1-1} + 1+0 = -400 \cdot x^{-2}+1 = \\\\= 1-\frac{400}{x^2}$

Приравняем ее к нулю:

$\displaystyle 1-\frac{400}{x^2} = 0\\\\\frac{x^2-400}{x^2} = 0\\\\\frac{(x-20) \cdot (x+20)}{x^2} =0\\\\\left[\begin{array}{ccc}x=20\\x=-20\end{array}\right$

(При этом $x \neq 0$)

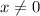Дальше определяем знаки производной на числовой прямой:

+++++++++++ [-20] --------------- (0) --------------- [20] +++++++++

Как видим, точки экстремума - это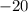 $-20$ и $20$.

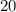Но точкой минимума является именно вторая точка, так как при переходе через эту точку знак меняется с "-" на "+".

В ней значение функции равно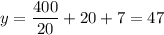 $y = \dfrac{400}{20} + 20 + 7 = 47$.

Задача решена!

ответ:  20.