Алгебра: 5ab2/b2-4a2 b-2a/ab при b=3.2 a= -0.6 Решите нужно

5ab2/b2-4a2 b-2a/ab при b=3.2 a= -0.6
Решите нужно

👇

Увидеть ответ

Ответ:

Evgenn4ik

10.10.2020

2,96

Объяснение:

5*(-0,6)*3,2/3,2*2-4*(-0,6)*2*3,2-2*(-0,6)/(-0,6)*3,2=2,96

4,6(12 оценок)

Открыть все ответы

Ответ:

youlia86

10.10.2020

104° - тупой угол, только один в треугольнике.

180°-104°=76° - сумма двух других углов. они равны, т.к. треугольниу равнобедренный.

76°:2=38° - углы при основании равнобедренного треугольника.

а) Сумма острых углов прямоугольного треугольника равна 90°.

90-30=60° - величина второго угла

Т.к. EF - биссектриса, то

60°:2=30° - ∠DEF

ED - основание ΔDEF, ∠DEF=∠EDF, EF=DF, следовательно, треугольник равнобедренный.

б) СF<DF

х см - длина одной стороны

х+17 см - длина другой стороны.

Р=77 см

Примем большую сторону за основание.

х+х+х+17=77

3х=77-17

3х=60

х=20(см) - длина равных сторон

20+17=37(см) - длина основания

Теперь примем за основание меньшую сторону.

х+2*(х+17)=77

х+2х+34=77

3х=43

х≈14,3(см) - длина основания

14,3+17=31,3(см) - длина каждой из двух других сторон.

4,6(70 оценок)

Ответ:

Xzxzxzxzxzzxzxz

10.10.2020

Уравнение четвёртой степени имеет вид:
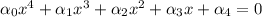
$\alpha _0x^4+ \alpha _1x^3+ \alpha _2x^2+ \alpha _3x+ \alpha _4=0$
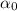Разделим обе части на коэффициент $\alpha _0$ , получаем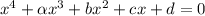
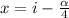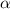$x^4+ \alpha x^3+ bx^2+cx+d=0$
где a, b, c, d – произвольные вещественные числа.

Уравнения вида приводится уравнение четвёртой степени, у которых отсувствует третьей степени., поэтому нужно сделать замену переменных, тоесть
$x=i- \frac{ \alpha }{4}$ , где $\alpha$ - коэффициент перед х^3 и 4 - произвольные вещественные числа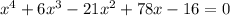

В нашем случае такое уравнение: x^4+6x^3-21x^2+78x-16=0

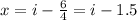Заменим $x=i- \frac{6}{4} =i-1.5$ , получаем
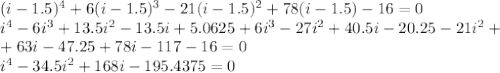
$(i-1.5)^4+6(i-1.5)^3-21(i-1.5)^2+78(i-1.5)-16=0\\ i^4-6i^3+13.5i^2-13.5i+5.0625+6i^3-27i^2+40.5i-20.25-21i^2+\\+63i-47.25+78i-117-16=0\\ i^4-34.5i^2+168i-195.4375=0$

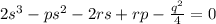
Получаем кубическое уравнение: $2s^3-ps^2-2rs+rp- \frac{q^2}{4}=0$
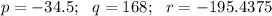
В нашем случае: $p=-34.5;\,\,\,\,q=168;\,\,\,\,r=-195.4375$
Подставляем и получаем уравнение
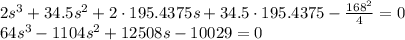
$2s^3+34.5s^2+2\cdot195.4375s+34.5\cdot195.4375- \frac{168^2}{4}=0\\ 64s^3-1104s^2+12508s-10029=0$
Разложим одночлены в сумму нескольких
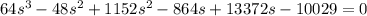
64s^3-48s^2+1152s^2-864s+13372s-10029=0

Выносим общий множитель
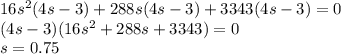
$16s^2(4s-3)+288s(4s-3)+3343(4s-3)=0\\ (4s-3)(16s^2+288s+3343)=0\\ s=0.75$
Уравнение 16s²+288s+3343=0 решений не имеет, так как D<0

Таким образом для решения уравнения остается квадратное уравнение
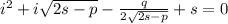
$i^2+i \sqrt{2s-p} - \frac{q}{2\sqrt{2s-p}}+s=0$
Заменяем
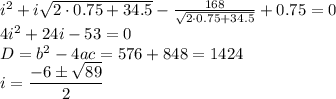
$i^2+i\sqrt{2\cdot0.75+34.5}- \frac{168}{\sqrt{2\cdot0.75+34.5}} +0.75=0\\ 4i^2+24i-53=0\\ D=b^2-4ac=576+848=1424\\ i= \dfrac{-6\pm \sqrt{89} }{2}$

Возвращаемся к замене
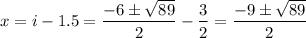
$x=i-1.5=\dfrac{-6\pm \sqrt{89} }{2}- \dfrac{3}{2} =\dfrac{-9\pm \sqrt{89} }{2}$

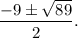
Окончательный ответ: $\dfrac{-9\pm \sqrt{89} }{2}.$