Вероятность попадания в мишень одного стрелка при одном выстреле для первого стрелка равна 0.8, для второго стрелка – 0.85. Стрелки произвели по одному выстрелу в мишень. Считая попадание в цель для отдельных стрелков событиями независимыми, найти вероятность события А – ровно одно попадание в цель.
Решение.
Рассмотрим событие A - одно попадание в цель. Возможные варианты наступления этого события следующие:
Попал первый стрелок, второй стрелок промахнулся: P(A/H1)=p1*(1-p2)=0.8*(1-0.85)=0.12
Первый стрелок промахнулся, второй стрелок попал в мишень: P(A/H2)=(1-p1)*p2=(1-0.8)*0.85=0.17
Первый и второй стрелки независимо друг от друга попали в мишень: P(A/H1H2)=p1*p2=0.8*0.85=0.68
Тогда вероятность события А – ровно одно попадание в цель, будет равна: P(A) = 0.12+0.17+0.68 = 0.97
Объяснение:
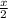книг, а на второй увеличить их число в двое - 2у книг, то на двух полках будет 180 книг: 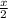+ 2у=180 (второе уравнение).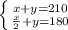
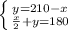
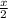+ 2*(210-x)=180 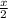-2х=180-420 - 
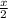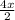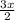=-240
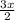= -240 = 240
1) x²+7x-18=0 → D=49+4•18=49+72=121 →
x1=(-7+11)/2 → x1=3/2 → x1=1,5
x2=(-7-11)/2 → x2=-18/2 → x2=-9
2) x²=2x+8 → x²-2x-8=0 →D=4+4•8=36 →
x1=(2+6)/2 → x1=8/2 → x1=4
x2=(2-6)/2 → x2=-4/2 → x2=-2
3) 25x²-1=0 → (5x-1)(5x+1)=0 →
5x-1=0 → 5x=1 → x=0,2
5x+1=0 → 5x=-1 → x=-0,2
4) 2x²-10x=0 → 2x(x-5)=0
2x=0 → x=0
x-5=0 → x=5
5) (x+10)²=(5-x)² → x²+20x+100=25-10x+x² → x²-x²+20x+10x+100-25=0 → 30x+75=0 → x=-75/30 → x=-2,5