Решите уравнение
(X+1)^2/3-(X-1)/2=(8X-1)/6
(X+1)^2/3-(X-1)/2=(8X-1)/6 |*6
2(X+1)^2-3(X-1)=8X-1
2x^2+4x+2-3x+3-8x+1=0
2x^2-7x+6=0
D=49-4*2*6=1
x=1,5
x=2
Решите уравнение
(2X-3)^2-2(5X-4)(X+1)=-9-13X
(2X-3)^2-2(5X-4)(X+1)=-9-13X
4x^2-12x+9-2(5x^2+5x-4x-4)+9+13x=0
4x^2-12x+9-10x^2-10x+8x+8+9+13x=0
6x^2+x-26=0
D=1-4*6*(-26)=625
x=-13/6
x=2
Не вычисляя корней квадратного уравнения, решите уравнение
1) 3X^2-2X-6=0
y(первое)=3X^2-2X-6
y(второе)=0
найдем координаты вершины параболы:
x(в)=-b/2a=2/6=1/3
y(в)=3(1/3)^2-2(1/3)-6=-19/3
координаты:(-19/3)
по формуле раскладываем sin3x и cos 4x, получаем sinx (3sinx-4sin^3x)+ 8cos^4x-8cos^2x+1; -8cos^2x выносим за скобку, так же выносим за скобку 4sinx получаем 4sin^2x (3/4-sin^2x)- 8cos^2x(1-cos^2x)+1 видим, что 1-cos^2x=sin^2x, в первую скобку добавим +1 -1 получим:4sin^2x (3/4+1-1-sin^2x)- 8cos^2x*sin^2x+1 в первой скобке видим 1-sin^2x=cos^2x, далее раскрываем первую скобку 4sin^2x*(-1/4)+4sin^2xcos^2x- 8cos^2x*sin^2x+1, упростим выражения с синкос получим: -sin^2x-4sin^2xcos^2x+1, вспоминаем,что cos^2x=1-sin^2x, получаем cos^2x-4sin^2xcos^2x, 4cos^2x за скобку получаем 4cos^2x(1/4-sin^2x), добавим в скобку +1-1 получим 4cos^2x (-3/4+cos^2x), раскроем скобку -3cos^2x +4cos^4x, -cosx за скобку получим cosx*cos3x=0 затем приравниваем поочередно к нулю cosx и cos3x и записываем из табл ответ.
Объяснение:
P.s если я тебе сделайте мой ответ лучшим для продвижения
Объяснение:
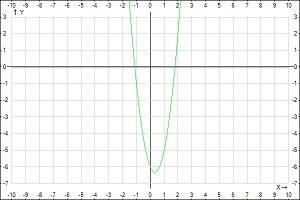
1) квадратичная, парабола
2) (0;1)
3) (-2;-3)
4) [-3;+беск)