Для решения этой задачи мы будем использовать комбинаторику, а именно комбинации.
Комбинация - это упорядоченный набор из нескольких элементов, где порядок не важен.
Разберем пошагово, как решить данную задачу.
Шаг 1: Сначала найдем сколько различных способов можно выбрать 4 мальчиков из 12.
Для этого мы можем использовать формулу для комбинации чисел: C(n, k) = n! / (k!(n-k)!), где n - общее количество элементов, k - количество выбираемых элементов.
Таким образом, мы можем рассчитать, сколько способов выбрать 4 мальчика из 12: C(12, 4) = 12! / (4!(12-4)!) = (12*11*10*9) / (4*3*2*1) = 495.
Итак, у нас есть 495 способов выбрать 4 мальчика из 12.
Шаг 2: Теперь найдем сколько различных способов можно выбрать 2 девочек из 5.
Аналогично, используем формулу для комбинации: C(5, 2) = 5! / (2!(5-2)!) = (5*4) / (2*1) = 10.
Итак, у нас есть 10 способов выбрать 2 девочки из 5.
Шаг 3: Найдем общее количество способов выбрать 4 мальчика и 2 девочки.
Для этого умножим количество способов выбрать мальчиков (495) на количество способов выбрать девочек (10): 495 * 10 = 4950.
Итак, общее количество различных способов выбрать 4 мальчика и 2 девочки составляет 4950.
Ответ: Можно выбрать 4 мальчика и 2 девочки из школьного кружка по шашкам 4950 различными способами.
Для решения данной задачи мы должны определить общее количество способов выбрать три цветка из вазы, а затем посчитать количество способов выбрать три цветка без нарциссов. Далее мы можем использовать эти два значения для определения вероятности.
Первым шагом определим общее количество способов выбрать три цветка из вазы. Мы можем использовать формулу сочетаний:
nCr = n! / (r!(n-r)!)
Где n - общее количество объектов (11 цветков в нашем случае), а r - количество объектов, которые мы выбираем (3 цветка).
Используя данную формулу, мы можем рассчитать:
Общее количество способов выбрать три цветка из вазы = 11! / (3!(11-3)!) = 165
Далее нам нужно определить количество способов выбрать три цветка без нарциссов. Мы можем просто вычесть количество способов выбрать три гвоздики (без нарциссов) из общего количества способов выбрать три цветка.
Количество способов выбрать три гвоздики = 5! / (3!(5-3)!) = 10
Теперь мы можем определить вероятность выбрать по крайней мере один нарцисс, используя эти два значения:
Вероятность выбрать по крайней мере один нарцисс = 1 - (вероятность выбрать три гвоздики / общее количество способов выбрать три цветка)
= 1 - (10 / 165)
= 1 - 0.0606
= 0.9394
Таким образом, вероятность того, что среди трёх случайным образом вынутых цветков окажется по крайней мере один нарцисс, составляет 0.9394 или около 94%.
Відповідь:
41
Пояснення:
(39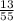 + 11
+ 11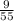 ) + (3
) + (3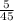 - 12
- 12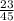 ) = 50
) = 50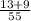 - (9
- (9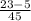 ) = 50
) = 50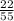 - 9
- 9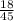 = 50
= 50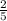 - 9
- 9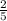 = 41
= 41